Diagnosegeleitete Förderung im inklusiven Mathematikunterricht der Grundschule – Professionalisierung durch reflektierte Handlungspraxis in der Lehrer*innenbildung

Diagnosis-oriented support in inclusive mathematics on the primary level – professionalization through reflective practice in teacher education

Autor/innen

  • Kristina Hähn Universität Duisburg-Essen
  • Uta Häsel-Weide Universität Paderborn
  • Petra Scherer Universität Duisburg-Essen

DOI:

https://doi.org/10.21248/qfi.72

Schlagworte/Keywords

Professionalisierung, Lehrer*innenbildung, Diagnose, Förderung, inklusiver Mathematikunterricht, professionalization, teacher education, diagnosis, support, inclusive mathematics

Zusammenfassung

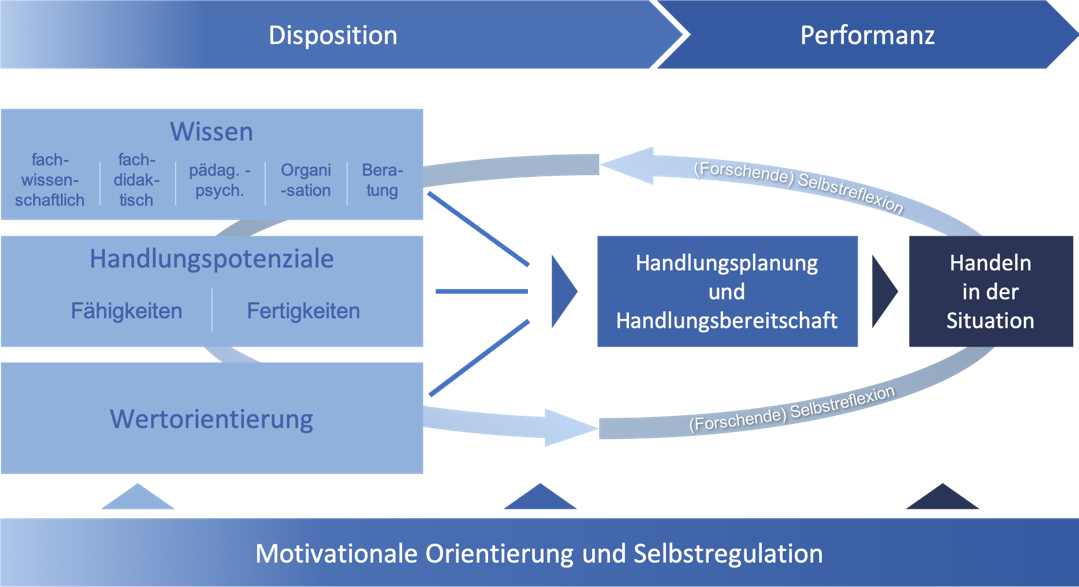
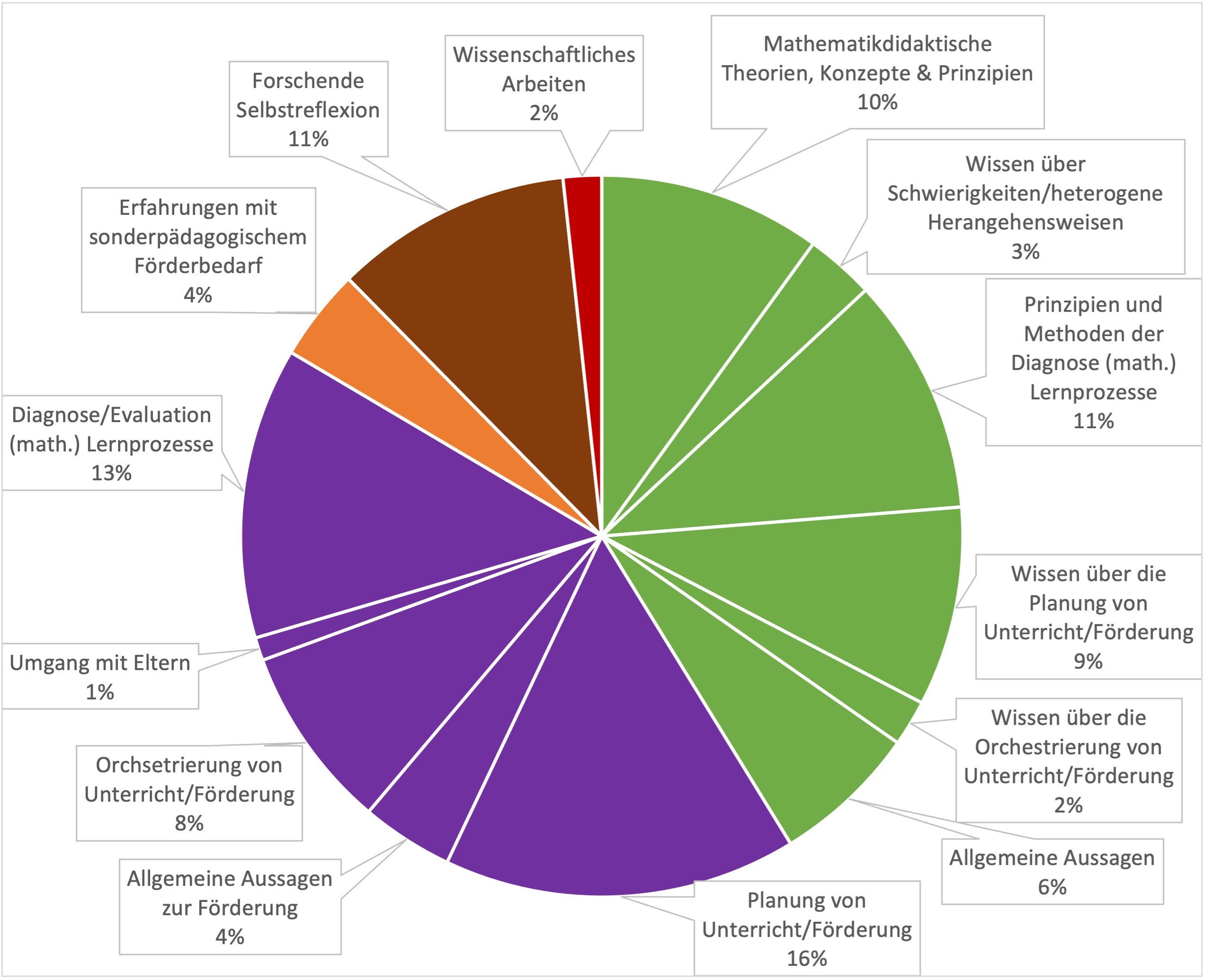
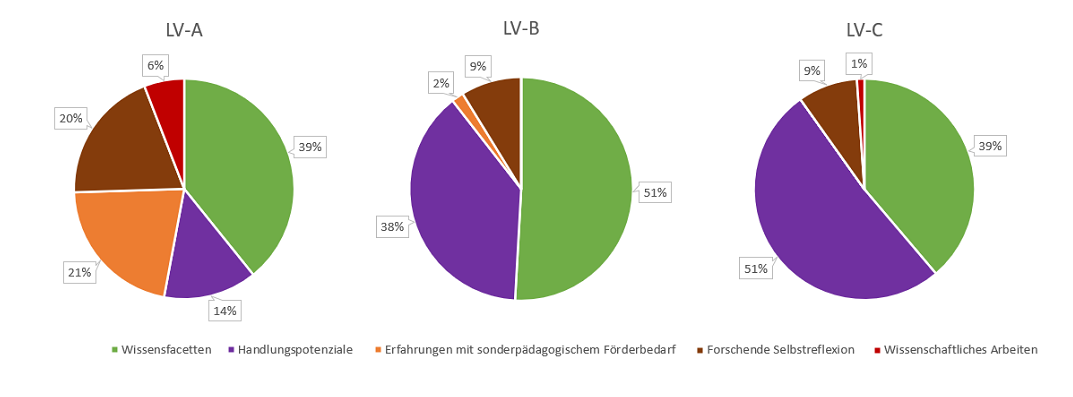
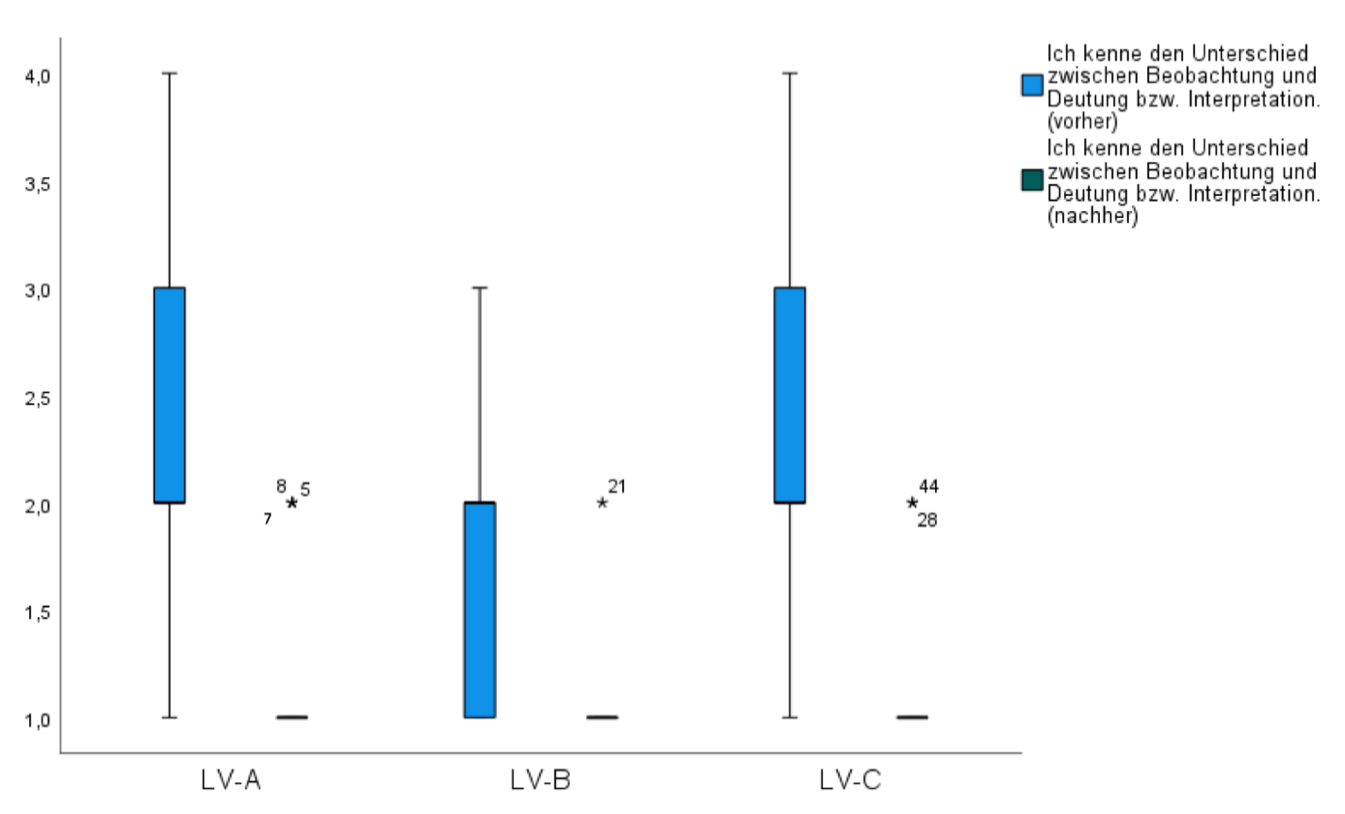
Für den inklusiven Unterricht ist es von großer Bedeutung, dass Lehrkräfte individuelle Potenziale und Fähigkeiten aller Schüler*innen erkennen, fördern und (weiter)entwickeln. Bereits in der ersten Phase der Lehrer*innenbildung können Lehrveranstaltungen so gestaltet werden, dass grundlegende und handlungsnahe Kompetenzen zu Diagnose und Förderung erworben und gleichzeitig eigene Professionalisierungsprozesse reflektiert werden können. Der Beitrag stellt die Konzeption von Lehrveranstaltungen vor, die die (reflexive) Vermittlung fach- und fachdidaktischer sowie pädagogischer Wissensbereiche und reflektierter Praxiserfahrungen in der Diagnose und Förderung von Kindern mit besonderen Schwierigkeiten zum Ziel haben. Die Begleitforschung der Lehrveranstaltungen fokussiert über einen Fragebogen mit offenen und geschlossenen Items die retrospektive Selbsteinschätzung des eigenen Kompetenzzuwachses der Studierenden. Die Ergebnisse der qualitativen und quantitativen Auswertung zeigen, dass in den fachbezogenen Lehrveranstaltungen der Kompetenzzuwachs facettenreich wahrgenommen wird und dies sowohl im Bereich des Wissens als auch des Handlungspotenzials. Zudem zeigen die Ergebnisse, dass mit Varianten solcher Veranstaltungskonzepte, die vergleichbare zentrale Gestaltungselemente aufweisen, ähnliche Ziele erreicht werden können.

 

Abstract

For teaching in inclusive settings, teachers have to identify, support, and develop the individual potentials and abilities of all pupils. Even in the first phase of teacher education, courses can be designed in that way, that basic and action related competencies with respect to diagnosis and support can be acquired, and at the same time own professionalization processes can be reflected. The paper presents the central ideas of teacher education courses that aim at (reflective) education of content knowledge, pedagogical content knowledge, and pedagogical knowledge as well as reflective practical experiences with respect to diagnosis and support for pupils with specific difficulties. For the accompanying research of the courses a questionnaire with open and closed items was used, focusing on the retrospective self-assessment of student teachers’ own competence development. The results of the qualitative and quantitative analysis show that the reported increase of competencies in the subject specific courses is perceived multifaceted, and this is true for the field of knowledge as well as for the potential for action. Moreover, the results show that variations of course conceptions with similar central design elements might reach comparable objectives.

Downloads

Veröffentlicht

2022-04-13

Ausgabe

Bd. 3 Nr. 2 (2021): Diagnostik

Rubrik

Artikel

Lizenz

Copyright (c) 2022 Kristina Hähn, Uta Häsel-Weide, Petra Scherer

Creative-Commons-Lizenz
Dieses Werk steht unter der Lizenz Creative Commons Namensnennung - Keine Bearbeitungen 4.0 International.

Einleitung

Für die inklusionsbezogene Gestaltung von Unterricht sind vielfältige Kompetenzen erforderlich, die Lehramtsstudierende im Hinblick auf ihr zukünftiges Berufsfeld erwerben müssen (vgl. z. B. Scherer, 2022). Unter anderem sind Lehrkräfte gefordert, den individuellen Lernstand der Schüler*innen zu ermitteln und mit ihnen zu besprechen, nächste Schritte festzulegen und passende Lernangebote zu machen sowie den Lernprozess zu beobachten (vgl. Kultusministerkonferenz, 2015). Angehende Lehrkräfte sind für diese diagnosegeleitete Förderung zu qualifizieren und die „Befähigung zu einem professionellen Umgang mit Vielfalt insbesondere mit Blick auf ein inklusives Schulsystem“ ist curricular zu verankern (Ministerium für Schule und Weiterbildung, 2020, §2, Abs.2). Diese Grundqualifizierung soll es zukünftigen Lehrkräften ermöglichen, das Lernen von Lernenden mit unterschiedlichen Potenzialen, Zugangsweisen und Lebenslagen professionell zu gestalten. Bereits in der Umstellung des Lehramtsstudiums auf die BA-/MA-Struktur wurde der Bereich der Diagnose und Förderung als verpflichtendes Element festgehalten, und auch in den erweiterten KMK-Standards für die Lehrerbildung (Kultusministerkonferenz, 2019) ist die diagnostische Kompetenz von Lehrkräften als Standard formuliert und operationalisiert. Dies gilt es in Bezug zur Mathematikdidaktik auszugestalten, da zwar im inklusiven Kontext der ganzheitliche Blick auf das Kind, seine Persönlichkeits- und Lernentwicklung eine zentrale Alltagsanforderung darstellt, die präzise Erfassung des Lernstands jedoch stets mit Blick auf die spezifischen fachlichen Gegenstände ausgestaltet werden muss. [1]

Für das Lehramtsstudium ergibt sich damit die Aufgabe, Studierenden Angebote zu machen, entsprechende Kompetenzen zu erwerben, damit sie auf der Basis einer Grundqualifizierung angemessen vorbereitet in den lebenslangen Prozess der Professionalisierung starten können, der von einer stetigen Weiterentwicklung z. B. auf der Basis von Reflexion, der Auseinandersetzung mit Krisen oder des gezielten Wissensausbaus durch Fortbildung geprägt ist (vgl. z. B. Terhart, 2000). [2]

In diesem Beitrag werden Möglichkeiten aufgezeigt, wie mathematikdidaktische Lehrveranstaltungen in der ersten Phase der Lehrer*innenbildung so gestaltet werden können, dass einerseits grundlegende diagnostische Kompetenzen bezogen auf das Fach Mathematik aufgebaut werden, die Studierenden anderseits durch die Konzeption der Veranstaltungen einen Professionalisierungsprozess durchlaufen und reflektieren, der bezogen auf das lebenslange Lernen als prototypisch betrachtet werden kann. Empirisch wird dies mit Hilfe der individuellen Selbsteinschätzung des Kompetenzerwerbs der Studierenden betrachtet. [3]

Diagnose und Förderung im inklusiven Mathematikunterricht

Soll der Heterogenität in einem inklusiven Fachunterricht Rechnung getragen werden, sind eine geeignete, mathematikdidaktisch fundierte Diagnostik und diagnosebasierte Förderung von zentraler Bedeutung (vgl. Schäfer & Rittmeyer, 2015), um die Kompetenzen und Schwierigkeiten zu erfassen und den Unterricht lernförderlich für alle Kinder zu gestalten. Dabei existiert eine Bandbreite an Verfahren und Diagnosemöglichkeiten, die es für den jeweiligen Anlass auszuwählen gilt. Das Spektrum an diagnostischen Methoden (vgl. Rottmann, Wellensiek & Lüken, 2018⁠; Schiefele, Streit & Sturm, 2019) bewegt sich dabei zwischen Polen: z. B. standardisiert versus nicht standardisiert, prozess- versus produktorientiert, kompetenz- versus defizitorientiert (vgl. auch Scherer, 2020). Für zukünftige Lehrkräfte ist die Kenntnis verschiedener Methoden wichtig, um sowohl standardisierte Instrumente kompetent anwenden zu können als auch individualisiert und unterrichtsnah zu diagnostizieren. Im Gegensatz zu einer traditionellen Diagnostik mit dem Ziel der Selektionsfunktion steht im Zentrum unterrichtsnaher Diagnosemethoden eine lernprozessbegleitende ganzheitliche kompetenzorientierte Betrachtung der Entwicklungsstände und -potenziale von Lernenden (vgl. Moser Opitz & Nührenbörger, 2015⁠; Selter, 2017). [4]

Eine Diagnose beschreibt dabei einen Ist-Zustand und stellt die Basis für eine Förderung dar, die allerdings nicht direkt aus der Diagnose abgeleitet werden kann. Förderung sowie der Unterricht insgesamt verfolgt jedoch immer ein Ziel, d. h. einen Soll-Zustand (vgl. Moser Opitz, 2010⁠; Wember, 1998), welcher zunächst auf der Grundlage fachdidaktischen Wissens über zentrale oder nächste Ziele und eine sinnvolle Abfolge der Inhalte aufgestellt werden muss. Pott (2019) spricht hier von der Notwendigkeit einer diagnostischen Deutung, zu der die Kompetenzen benötigt werden, „um aus erhobenen Diagnoseergebnissen angemessene und wirksame weiterführende Maßnahmen zu entwickeln, unabhängig davon, ob es sich dabei um tiefergreifende Diagnosen oder aber Förderansätze handelt“ (Pott, 2019, S. 103). Konkret bedeutet dies, dass etwa bei der Beobachtung von zählendem Rechnen beachtet werden muss, ob dies von einem Kind im Kindergartenalter gezeigt wird oder einem Grundschulkind im dritten Schuljahr. Um für Lernende im dritten Schuljahr eine Förderung zur Ablösung vom zählenden Rechnen zu planen, müssen Lehrkräfte z. B. fachdidaktisches Wissen darüber haben, welche Alternativen es zum zählenden Rechnen gibt, welche Bedeutung Zahl- und Operationsvorstellungen einnehmen und welche Arbeits- und Anschauungsmittel genutzt werden können (Häsel-Weide, Nührenbörger, Moser Opitz & Wittich, 2019). Dabei können sich weitere diagnostische Fragen z. B. zur Zahlvorstellung, zur Mengenerfassung oder zum Operationsverständnis des Förderkinds ergeben. Für mathematikdidaktische Lehrveranstaltungen bedeutet dies, dass auf der Basis der Diagnose die Planung und Durchführung von Förderung als damit verknüpft betrachtet wird (vgl. Geisen, 2021, S. 69f.⁠; Hoth, Döhrmann et al., 2016, S. 43). Lernprozessbegleitend fließen stets weitere Erkenntnisse in Förderprozesse ein. Diesbezügliche Interaktionen oder Handlungen entwickeln sich daher dynamisch aufgrund der diagnostischen Schlussfolgerungen. [5]

Lehrkräfte müssen also in der Lage sein, sowohl bei der Durchführung als auch bei der Auswertung und den Folgerungen für die Förderung kompetent zu agieren, und insbesondere sind fachliche und fachdidaktische Kompetenzen erforderlich, um Diagnosen durchzuführen, zu interpretieren und zu reflektieren sowie generell Lernprozesse im Fachunterricht angemessen zu initiieren, zu begleiten und diagnosegeleitet zu evaluieren. Zentral sind dabei Kenntnisse über mathematische Vorstellungen, Vorgehensweisen und Entwicklungen von Lernenden sowie über typische Hürden, die dabei überwunden werden müssen (vgl. Häsel-Weide & Prediger, 2017). [6]

Professionalisierung für diagnosegeleitete Förderung im Fach Mathematik

Modell der Professionalisierung

Die Entwicklung von Expertise für (inklusiven) Mathematikunterricht bedarf des Aufbaus und der (reflexiven) Vermittlung zwischen unterschiedlichen Wissensvorräten wie pädagogischem, fachwissenschaftlichem und fachdidaktischem Wissen und reflektierter Praxiserfahrung. Für die Professionalisierung sind die unterschiedlichen Wissensformen in Verflechtung mit Erfahrungswissen aufzubauen und reflexiv miteinander in Beziehung zu setzen (vgl. Baumert & Kunter, 2006⁠; Terhart, 2011). Reis und Seitz (2019) beschreiben auf der Grundlage der Modelle von Baumert und Kunter (2006) sowie von Fröhlich-Gildhoff, Nentwig-Gesemann und Pietsch (2011) ein Modell zum Erwerb „reflexiven Theorie- und Handlungswissens im Verbund mit einem forschenden Habitus“ (Reis & Seitz, 2019), das bspw. an der Universität Paderborn das Gerüst für eine inklusionsbezogene Qualifizierung bildet (vgl. Abb. 1). [7]

Abbildung 1: Verknüpfungsmodell der Professionalisierung inklusionsbezogenen Handelns von Lehrpersonen (Reis & Seitz, 2019, o. S. in Anlehnung an Baumert & Kunter, 2006 sowie Fröhlich-Gildhoff et al., 2011⁠; vgl. auch Filipiak, 2020)

Der Bereich Wissen wird in Anlehnung an Baumert und Kunter (2006) unterteilt in Fachwissen, fachdidaktisches Wissen, pädagogisch-psychologisches Wissen, Organisationswissen und Beratungswissen. In Anlehnung an das Modell von Fröhlich-Gildhoff et al. (2011) wird im Bereich der Disposition neben dem Wissen die Wertorientierung und das Handlungspotenzial herausgestellt, worunter prozedural-methodisches Wissen (z. B. bezogen auf didaktisches Vorgehen, Diagnostik) und soziale Fähigkeiten (z. B. Perspektivübernahme und Empathiefähigkeit) fallen (vgl. Fröhlich-Gildhoff, Weltzien, Kirstein, Pietsch & Rauh, 2014, S. 10). Das wechselseitige Zusammenspiel der Facetten der Disposition wirkt sich auf die Handlungsplanung und bereitschaft aus, die den Übergang zur konkreten Handlung in der jeweiligen Situation, also der Performanz, darstellt. Die (forschende) Selbstreflexion verbindet beide Ebenen miteinander und macht zugleich deutlich, dass über die reflektierte Erfahrung die Expertise der Lehrkräfte ausgebaut wird. Sie ist von zentraler Bedeutung, da an dieser Stelle das Nachdenken über die Wirkung des eigenen Handelns im Kontext der Lehr-/Lernkultur des Unterrichts in der Institution Schule zu einem Antrieb für die eigene (Weiter)Entwicklung werden kann. Deshalb ist bereits die Universität aufgefordert, Studierende z. B. im Rahmen des forschenden Lernens in diesen Prozess einzuführen und so einen Zugang zum eigenen professionellen Handeln zu ermöglichen (Häsel-Weide, Seitz, Wallner, Wilke & Heckmann, 2021⁠; Reis & Seitz, 2019). [8]

Eine Erläuterung und Diskussion des Modells hinsichtlich der inklusiven Hochschullehre findet sich bei Filipiak (2020), eine fachbezogene Konkretisierung des Modells bezüglich Diagnose und Förderung (im inklusiven Mathematikunterricht) existiert bislang nicht. Auch andere Professionalisierungsmodelle liefern keine einheitlichen Modelle, vielmehr wird die diagnostische Kompetenz i. d. R. mit Bezug auf das Modell von Baumert und Kunter (2006) in einigen Modellierungen als ein eigenständiger Wissensbereich aufgefasst, während andere es als Facette mehrerer Wissensbereiche verstehen (vgl. zusammenfassend Geisen, 2021, S. 63⁠; auch Leuders, Dörfler, Leuders & Phillip, 2018⁠; Rottmann et al., 2018) und ihren Studien zu Grunde legen. [9]

Forschungsstand

Aktuelle Arbeiten der Mathematikdidaktik (bspw. Geisen, 2021⁠; Heinrichs, 2015⁠; Hoth, 2016⁠; Philipp, 2018⁠; Pott, 2019⁠; Reinhold, 2018) beschreiben und erforschen diagnostische Kompetenzen von (zukünftigen) Lehrkräften national vielfach in Anlehnung an die Kompetenzmodellierung von Baumert und Kunter (2006). Mit Bezug auf dieses Modell wird diagnostische Kompetenz als eine inhaltliche Spezifizierung des umfassenderen Kompetenzbegriffs gefasst und beinhaltet somit alle kognitiven und affektiv-motivationalen Fähigkeiten zur Wahrnehmung und Interpretation relevanter inhaltlicher Aspekte sowie daraus entwickelte Schlussfolgerungen (vgl. Hoth, Döhrmann et al., 2016, S. 43). Hier kommt pädagogisch-psychologisches Wissen in Verbindung mit fachlichem und fachdidaktischem Wissen in Bezug zu den Spezifika bestimmter Inhaltsbereiche zur Anwendung, was als diagnostische Kompetenz konzeptualisiert wird (vgl. Moser Opitz, 2006). Beide Bereiche werden dabei von individuellen Überzeugungen beeinflusst, bspw. zur Struktur der Mathematik, zum Erwerb mathematischen Wissens sowie zu fächerübergreifenden personen- und kontextbezogenen Aspekten (vgl. Geisen, 2021, S. 72f.). [10]

Studienergebnisse zu Diagnosekompetenzen von Lehrkräften verdeutlichen, dass Lehrkräfte mathematische, mathematikdidaktische und pädagogische Wissensgrundlagen nutzen und dies Einfluss auf deren eingenommene Perspektive in der Wahrnehmung, Interpretation und Gestaltung von Unterricht hat (vgl. Hoth, 2016, S. 313ff.⁠; Philipp, 2018). Auch die Kenntnis von Diagnosemethoden ist für diagnostische Kompetenzen von Bedeutung (vgl. Philipp, 2018, S. 125). Die TEDSFU-Studie zeigt zudem, dass Diagnosen von Lehrkräften gemäß der eigenen inhaltspezifischen oder allgemeinpädagogischen Expertise eher fachlich-bewertend oder schülerorientiert-handlungsbezogen ausfallen können (vgl. Hoth, Döhrmann et al., 2016). Dennoch scheint es ein Zusammenspiel verschiedener Kompetenzen zu geben, denn es wird vermutet, dass Lehrkräfte versuchen, ihr fehlendes fachliches bzw. fachdidaktisches Wissen möglicherweise durch ihr fachunabhängiges pädagogisches Wissen oder ihre Berufs- bzw. Unterrichtserfahrung teilweise zu kompensieren (vgl. Geisen, 2021, S. 279). Diagnostische Kompetenzen und solche zur Förderung müssen darüber hinaus in keinem direkten Zusammenhang stehen. So konnte bspw. Schulz (2014, S. 406f.) zeigen, dass es keinen zwingenden Zusammenhang zwischen der identifizierten Diagnosekompetenz von Lehrkräften beim Erkennen von Schwierigkeiten und deren Kompetenzen zur Planung inhaltlich angemessener Fördermaßnahmen gibt. [11]

Kompetenzerwerb in universitären Lehrveranstaltungen

Neben der Erhebung diagnostischer Kompetenzen bei Lehrkräften wird als bedeutsam erachtet, wie der Erwerb bzw. die Entwicklung innerhalb universitärer Lehrveranstaltungen angeregt werden kann (vgl. Philipp, 2018, S. 125). Heinrichs (2015) konnte für die untere Sekundarstufe zeigen, dass diagnostische Kompetenzen zukünftiger Lehrkräfte während der universitären Lehrer*innenbildung gefördert werden können und dass hierzu praktische Erfahrungen hilfreich sind. Auch Pott (2019) untersuchte in einer explorativen Studie diagnostische Deutungen von Lehramtsstudierenden. Fokussiert wurde dabei insbesondere die Verbindung von Diagnoseergebnissen und deren Deutung mit der Entwicklung darauf aufbauender Fördermaßnahmen. Die Ergebnisse zeigen einen deutlichen Mehrwert durch die Kopplung von Theorie und Praxis in der Lehrer*innenbildung für den Kompetenzerwerb im Bereich der diagnostischen Deutung. [12]

In Bezug auf die Lehrer*innenbildung verweisen die Studien insgesamt auf die Sensibilisierung für die Wichtigkeit fachdidaktischer Theorien und mathematikdidaktischen Wissens sowie auf die Reflexion der Angemessenheit der Diagnosemethode, das Verständnis von Diagnose als mehrdeutigen Prozess und den kritischen Umgang mit eigenen Urteilen. In den Blick genommen werden sollte darüber hinaus auch die Beachtung sozialer Beziehungen zwischen an Diagnose und Förderung teilnehmenden Personen, denn diesen Aspekt beachteten Studierende nur wenig (vgl. Pott, 2019, S. 487). Für eine diagnostische Kompetenzentwicklung in der ersten Phase der Lehrer*innenbildung wird insgesamt die Kopplung verschiedener Aspekte als zentral betrachtet. Dazu gehört die Vermittlung von fachdidaktischem Wissen über Lernprozesse und Fehlvorstellungen zusammen mit (sonder)pädagogischem Wissen bzw. fachlichem und fachunabhängigem Organisations- und Methodenwissen, auf das in der Unterrichtsplanung zurückgegriffen werden kann (vgl. Geisen, 2021, S. 279⁠; Pott, 2019, S. 476ff.). Ebenso wird empfohlen, den Wissenserwerb über Lernschwierigkeiten und diesbezügliche Unterstützungsmaßnahmen integrierend zu behandeln (vgl. Schulz, 2014). Darauf bezogene Selbstreflexionsprozesse von Studierenden wurden bislang jedoch noch nicht in den Blick genommen. Diesem Desiderat wendet sich die im Folgenden dargestellte Studie zu. [13]

Design der Studie

Fragestellung

Die inhaltliche Analyse des Gegenstands ‚Diagnose und Förderung im Fach Mathematik’ sowie das zugrundeliegende Professionalisierungsmodell und der aktuelle Forschungsstand zeigen die Notwendigkeit einer vernetzten Qualifizierung von Lehrkräften im Studium auf. Der Wissensaufbau ist mit konkretem Handeln in diagnostischen und fördernden Situationen zu verknüpfen und mit den Studierenden fallbezogen zu reflektieren, um den Prozess der Professionalisierung an konkreten Situationen exemplarisch zu erleben. Wie oben bereits ausgeführt, stellt ‚Diagnose und Förderung’ ein festgeschriebenes Element im LABG dar (vgl. auch Häsel-Weide & Prediger, 2017), und diese Kombination von Diagnose und Förderung ist im Lehramtsstudium zu adressieren. [14]

Die hier vorgestellte, explorative Studie ist verortet in einem Kooperationsprojekt1 zur Qualifizierung von angehenden Lehrkräften im Bereich diagnosegeleiteter Förderung. Hierzu wurden Seminare entwickelt, die den Kompetenzerwerb im Bereich Diagnose und Förderung ermöglichen und dabei konkrete Handlungserfahrungen in den Mittelpunkt stellen. [15]

Dabei werden folgende Fragestellungen verfolgt, wobei erstere im Fokus dieses Beitrags steht: [16]

  1. Inwiefern nehmen angehende Lehrkräfte eine eigene Lernentwicklung im Rahmen der Veranstaltung wahr, und wie schätzen sie ihren Kompetenzzuwachs ein? [17]

  1. Welche Gestaltungselemente der Veranstaltung werden als lernförderlich wahrgenommen und als entscheidend für den Kompetenzerwerb angegeben? [18]

Inhalte und Struktur der Lehrveranstaltungen

Im Kontext der Studie wurden drei Lehrveranstaltungen (weiter)entwickelt und beforscht, die als gemeinsamen Schwerpunkt den fachbezogenen Kompetenzerwerb im Bereich Diagnose und Förderung aufweisen und die den Wissenserwerb mit Handlungserfahrungen kombinieren: Seminar ‚Diagnose und Förderung: Schüler*innen mit sonderpädagogischem Unterstützungsbedarf’ (LV-A, Universität Duisburg-Essen), Seminar ‚Diagnose und Förderung: Mathematische Förderung in der Schuleingangsphase – An individuelle Lernstände im Zahlenraum bis 20 anknüpfen’ (LV-B, Universität Duisburg-Essen) und Seminar ‚Zahlenstark – Lernentwicklungen diagnostizieren und fördern’ (LV-C, Universität Paderborn). Im Folgenden werden die zentralen konzeptionellen Merkmale der drei Lehrveranstaltungen vergleichend dargestellt. [19]

Grundlegender mathematischerInhaltsbereich: In allen drei Lehrveranstaltungen zielt der inhaltliche Schwerpunkt auf zentrale mathematische Inhaltsbereiche, die sich als Hürde beim Mathematiklernen erweisen können, wie die Begriffsbildung bzw. der Grundvorstellungsaufbau zu geometrischen Grundformen (LV-A) oder der Aufbau tragfähiger Zahl- und Operationsvorstellungen (LV-B, LV-C). Der jeweilige ausgewählte Schwerpunkt wird im Seminar inhaltlich vertieft und ist bereits in vorhergegangenen Semestern intensiv fachlich und fachdidaktisch grundgelegt. [20]

Verzahnung von Wissensfacetten: Die zentralen mathematischen Inhaltsbereiche werden verknüpft mit Wissensfacetten zu Diagnose und Förderung, bspw. indem diagnostische Aufgaben zu den mathematischen Bereichen thematisiert, entwickelt und analysiert werden. Auch Leitideen und Prinzipien der Förderung (vgl. Häsel-Weide & Nührenbörger, 2012⁠; Hess & Nührenbörger, 2017) werden inhaltsspezifisch konkretisiert und entsprechende Aufgabenstellungen und Materialien konzipiert. U. a. werden auch Theorien zur Interaktion (z. B. Krummheuer & Fetzer, 2010) sowie zum sprachsensiblen Fördern (z. B. Götze & Hang, 2017) miteinbezogen. Die gemeinsame Diskussion der Förderplanung bzw. Reflexion der durchgeführten Förderung kann dabei zu vertieften fachlichen und fachdidaktischen Kompetenzen beitragen. [21]

Reflektierte Praxiserprobungen: Die Lehrveranstaltungen sehen als zentrales Element eigene Praxiserprobungen der Studierenden vor und beinhalten einerseits die Analyse einer videographierten Lernstandserfassung eines Kindes, die zuvor durch ein semistrukturiertes, leitfadengestütztes Interview (vgl. bspw. Misoch, 2015) erhoben wurde, andererseits die Planung und konkrete Durchführung von Fördereinheiten auf der Basis der Lernstandserfassung und eine semesterbegleitende gemeinsame Analyse der kindlichen Lernprozesse und Reflexion der Förderung im Seminar. [22]

Alle drei Veranstaltungen werden durch einen inhaltlichen Block zu den Grundlagen ‚Schwierigkeiten beim Mathematiklernen’ und zu diagnostischen Methoden im Mathematikunterricht vorbereitet. Daran anschließend wird eine videographierte Diagnose ausgewertet, die zuvor von den Studierenden selbst (LV-A, LV-B) bzw. von der Seminarleitung (LV-C) durchgeführt wurde und bei dem ein Beobachtungsleitfaden (LV-B, LV-C; vgl. Häsel-Weide & Nührenbörger, 2017) zum Einsatz kommt. Im Vorfeld wird eine fachdidaktische Analyse der einzusetzenden Diagnoseaufgaben und Materialien vorgenommen. Auf der Basis der individuellen Diagnose formulieren und hierarchisieren die Studierenden, unterstützt und begleitet durch die Seminarleitung, Ziele für die Förderung und führen diese allein (LV-A) oder im Team (LV-B; LV-C) über einen Zeitraum von mehreren Wochen durch (LV-A: 5-6 Wochen; LV-B, LV-C: 10 Wochen). Mithilfe von Videoaufzeichnungen oder Beobachtungsprotokollen der Förderung wird sowohl eine Analyse der kindlichen Lernprozesse, des fach- und zielgerechten Einsatzes von Aufgabenstellungen und Medien als auch des eigenen Förderverhaltens initiiert und reflektiert. Semesterbegleitend werden immer wieder fachdidaktische Schwerpunkte thematisiert und mit den Vorgehensweisen und Vorstellungen der Förderkinder (u. a. auch anhand von Videovignetten aus vergangenen Veranstaltungen; LV-C) angereichert. [23]

Organisationsstruktur der Lehrveranstaltungen: Die Lehrveranstaltungen finden je nach Seminarkonzept im Lehramt Grundschule im Umfang von 3 SWS an der Universität (LV-A) oder in der Schule (LV-B) statt, oder aber verankert im Lehramt für sonderpädagogische Förderung mit 4 SWS im Lehr-Lern-Labor der Universität (LV-C). Während LV-B und LV-C Kinder mit Schwierigkeiten beim Mathematiklernen im Heterogenitätsspektrum inklusiver Settings betrachten, fokussiert LV-A explizit Lernende mit sonderpädagogischem Unterstützungsbedarf. [24]

Methodisches Vorgehen

Datenerhebung und Stichprobe

Mittels eines Fragebogens wurden die angehenden Lehrkräfte zu einer retrospektiven Selbsteinschätzung der im Rahmen der Veranstaltung erweiterten Kompetenzen aufgefordert. Der Fragebogen enthielt eine Kombination aus drei offenen Fragen und weiteren Items zur Einschätzung der eigenen Kompetenzentwicklung, basierend auf einer vier-stufigen Likert-Skala (1 = trifft zu; 4 = trifft nicht zu; vgl. Del Piero et al., 2019). In Anlehnung an die oben vorgestellten Modelle (Baumert & Kunter, 2006⁠; Fröhlich-Gildhoff et al., 2011⁠; Reis & Seitz, 2019) zur Beschreibung von Kompetenzen wurden dabei die Bereiche Wissen, Handlungspotenziale und Wertorientierung unterschieden. Insgesamt wurden 10 zentrale Lernziele operationalisiert und als Items im Fragenbogen aufgenommen. Beispielhaft sei für den jeweiligen Bereich ein Item gegeben: [25]

Wissen: Ich weiß um Schwierigkeiten, die bei Lernenden in einer Fördersituation auftreten können. [26]

Handlungspotenziale: Ich kann Lernende beim Entdecken durch geeignete, individuelle lernförderliche Impulse begleiten und so mathematisches Verstehen fördern. [27]

Wertorientierungen: Ich kann in Fördersituationen eine förderliche Lernatmosphäre schaffen. [28]

Zur Erfassung der lernförderlichen Aktivitäten der Veranstaltungen wurden die Studierenden aufgefordert, für jedes Item aus einer vorgegebenen Liste die Elemente der Lehrveranstaltung anzugeben, die ihrer Einschätzung nach zu dieser Kompetenzerweiterung beigetragen haben. Gemäß den Strukturelementen der Veranstaltung zählten dazu u. a. der Input der Lehrenden, die Planung der Diagnose & Förderung, die Beobachtung der Aktivitäten des Kindes, die eigene individuelle Videoanalyse oder auch die Präsentation & gemeinsame Analyse im Seminar (vgl. auch Scherer, 2022). [29]

Um die persönlichen Schwerpunkte des Kompetenzerwerbs unbeeinflusst von den vorgegebenen geschlossenen Items zu erfassen, wurde zu Beginn des Fragebogens das offene Item „Geben Sie möglichst konkret an, was Sie im Seminar ‚Diagnose und Förderung’ / ‚Zahlenstark’ gelernt haben.“ präsentiert. Im Anschluss an die geschlossenen Items wurde mit zwei weiteren offenen Items der Theorie-Praxis-Bezug fokussiert. [30]

Ein solches Vorgehen der Selbsteinschätzung erlaubt nur bedingt, von den Einschätzungen auf tatsächliche Kompetenzen zu schließen, die z. B. über Tests erhoben werden würden. „Dies bedeutet nicht, dass die in Selbsteinschätzung enthaltenen Informationen generell uninteressant oder unnütz wären; es muss lediglich beachtet werden, dass es sich hierbei nicht um eine Messung der interessierenden Kompetenz selbst handelt, sondern um ein diesbezügliches Selbstkonzept“ (Hartig & Jude, 2007, S. 26). In dieser Studie steht gemäß der Fragestellung gezielt der selbstberichtete bzw. selbsteingeschätzte Kompetenzzuwachs im Vordergrund, da es vor allem interessiert, welche Aspekte die Studierenden nennen und inwiefern sich die Konzeption der Veranstaltung mit der Möglichkeit, Handlungserfahrungen im Bereich Diagnose und Förderung zu machen und diese zu reflektieren, in besonderer Weise in der Einschätzung diesbezüglicher Kompetenzfacetten spiegelt. [31]

Die Fragenbögen wurden im Rahmen des Projekts in mehreren Schleifen überarbeitet und im Sommersemester 2018 und 2019 an jedem Standort durchgeführt. Für die Auswertung können 56 Fragenbögen herangezogen werden (LV-A, n = 13; LV-B, n = 12; LV-C, n = 31). [32]

Auswertungsmethodik

Offene Items

Zur Auswertung des offenen Items „Geben Sie möglichst konkret an, was Sie im Seminar ‚Diagnose und Förderung’ / ‚Zahlenstark’ gelernt haben.“ ist ein qualitatives Verfahren notwendig, das erlaubt, die Aussagen der Studierenden mit Blick auf die genannten Aspekte des eigenen Kompetenzerwerbs zu strukturieren, um Schwerpunkte zu identifizieren. Dazu wurde die strukturierende, qualitative Inhaltsanalyse nach Mayring (2010) eingesetzt. Abbildung 2 zeigt exemplarisch zwei Freitexte aus LV-B und LV-C. [33]

Abbildung 2: Beispielhafte Antworten zum offenen Item (LV-B und LV-C)

Die Freitexte von 55 Studierenden1 aus den drei Seminartypen wurden wie folgt analysiert. Die Texte wurden in Sinneinheiten gegliedert (i. d. R. Sätze bzw. Aufzählungspunkte; n = 314), und die Kategorienbildung wurde in einem mehrzyklischen Verfahren vorgenommen: Deduktiv wurden zunächst übergeordnete Kategorien in Anlehnung an das Modell der Professionalisierung (vgl. Abb. 1) gebildet und Textteile zugeordnet. In einem weiteren induktiven Schritt wurden Unterkategorien entwickelt, die feiner sind als die Unterteilung in z. B. fachdidaktisches und pädagogisch-psychologisches Wissen. Dadurch ist es einerseits möglich, inhaltlich aussagekräftigere Ergebnisse zu erhalten und andererseits Aussagen zum erworbenen Wissen und zu erworbenen Handlungspotenzialen parallel betrachten zu können. Die Auswertung zielt nicht darauf, einen (selbsteingeschätzten) Kompetenzzuwachs zu beschreiben, sondern zu erfassen, inwiefern in den Aussagen der Studierenden die verschiedenen Professionalisierungsaspekte zu finden sind und welchen Schwerpunkt die Studierenden in ihrer eigenen Entwicklung wahrnehmen. [34]

Handlungspotenziale und Wissensfacetten wurden gemäß dem Modell der Professionalisierung unterschieden, indem Aussagen dem Wissen zugeordnet wurden, wenn von Erkenntnissen gesprochen wurde, während Aussagen als Handlungspotenziale kodiert wurden, wenn die Studierenden Fähigkeiten beschrieben, die sie in den konkreten Handlungssituationen aufgebaut hatten. Damit ergaben sich auf der ersten Ebene folgende Kategorien (vgl. Tab. 1). [35]

Tabelle 1: Übersicht über Kategorien auf der ersten Ebene
Wissensfacetten Handlungspotenziale Forschende Selbstreflexion
Definition Aussagen bezogen auf Kenntnisse und Wissenselemente Aussagen bezogen auf Fähigkeiten und Fertigkeiten Aussagen bezogen auf Erkenntnisse zum eigenen Lernprozess
Ankerbeispiel „Außerdem habe ich gelernt, was für Kompetenzen in den verschiedenen mathematischen Bereichen von Kindern versch. Alters erreicht werden sollen“„Welche Unterbereiche zu den jeweiligen mathematischen Kompetenzen (z. B. Stellenwertverständnis) gehören“ „In der Fördersitzung flexibel reagieren können und spontan Aufgaben entwickeln“„Diagnoseinterview was durchgeführt wurde auszuwerten und daraus Lernziele aufzustellen“ „Wie ich selbst wirke und besser auf das Kind eingehen kann durch andere Formulierungen“„Anfangs dachte ich mir, dass ich mir einfach Aufgaben ausdenken kann und diese mit dem Schüler/in bearbeite. Erst nach den ersten Seminar-Sitzungen habe ich gelernt, dass diese aber auch Sinn ergeben müssen.“

Auf einer zweiten Ebene wurden die Wissenselemente und Handlungspotenziale bezogen auf die Aspekte von Diagnose und Förderung genauer analysiert. Dabei wurden in einer Kombination von deduktiven und induktiven Vorgehensweisen folgende Facetten des Wissens und der Handlungspotenziale unterschieden (vgl. Tab. 2; auch Pott, 2019). [36]

Bei der Codierung der Aussagen zeigten sich zwei unerwartete Phänomene. Einerseits nannten Studierende die Begegnung mit Kindern mit (sonder)pädagogischem Förderbedarf als Aspekt des Gelernten, i. d. R. ohne dass in den Aussagen Wissen über das Konstrukt oder Bezüge zum mathematischen Lernen deutlich wurden, sondern vor allem die Erfahrung genannt wurde („Ich persönlich habe zum 1. Mal eine Förderschule besucht (sonst waren es nur Regelschulen)“; „Auseinandersetzung mit Kindern, die einen Förderschwerpunkt haben“). Anderseits wurden Aspekte des wissenschaftlichen Arbeitens formuliert, die über den Inhaltsbereich Diagnose und Förderung hinausgingen und deshalb gesondert kategorisiert wurden („Sich Literatur zu dem Thema besorgen – eigenen Wissenshorizont erweitern“). Aufgrund der Vielzahl der Aussagen (n = 36) zu diesen Themen wurden dazu zwei eigene Kategorien vergeben. [37]

Tabelle 2: Übersicht über inhaltlich ausdifferenzierte Wissensfacetten und Handlungspotenziale zur diagnosegeleiteten Förderung
Wissensfacetten Handlungspotenziale
Mathematikdidaktische Theorien, Konzepte & Prinzipien
Wissen über Schwierigkeiten/heterogene Herangehensweisen
Prinzipien und Methoden der Diagnose (mathematischer) Lernprozesse Diagnose/Evaluation (mathematischer) Lernprozesse
Wissen über die Planung von Unterricht/Förderung Planung von Unterricht/Förderung
Wissen über die Orchestrierung von Unterricht/Förderung Orchestrierung von Unterricht/Förderung
Allgemeine Aussagen Allgemeine Aussagen zur Förderung
Umgang mit Eltern

Auswertung Skalierungsfragen

Ausgewertet werden konnten insgesamt die in Abschnitt 5.1 genannten 56 Fragebögen, und es erfolgte die Auswertung von 7 Ankeritems (bzw. sprachlich minimal abweichenden Items der ersten Version) zu den Kategorien Wissen (3 Items), Handlungspotenziale (3 Items) und Wertorientierung (1 Item), die in allen drei Lehrveranstaltungstypen zum Einsatz kamen. Verglichen wurde einerseits für jedes Item die Zielerreichung vor und nach dem Seminar durch retrospektive Selbsteinschätzung („Inwieweit haben Sie folgende Ziele erreicht? Schätzen Sie dabei einmal Ihre Kompetenzen vor der Teilnahme am Seminar ein und einmal nach der Teilnahme am Seminar.“). Zudem erfolgte ein Vergleich der Kategorien Wissen, Handlungspotenziale und Wertorientierung sowie ein Vergleich der drei Lehrveranstaltungen. Die Auswertung erfolgte mit SPSS und zusätzlich zum Signifikanztest wurde die Effektstärke anhand Wilcoxons r berechnet. [38]

Auch wenn hier nur eine geringe Stichprobe vorliegt, so können die Ergebnisse – flankierend zu den Ergebnissen des offenen Items – erste Hinweise auf die Kompetenzeinschätzungen der Studierenden in den drei unterschiedlichen Lehrveranstaltungen liefern. Diese Vergleiche sind natürlich sehr vorsichtig zu interpretieren. [39]

Ergebnisse

Schwerpunkte der eigenen Entwicklung

Die Auswertung des offenen Items führt zu Erkenntnissen, in welchen Bereichen die Studierenden ihre eigene Entwicklung wahrgenommen haben. Dabei ist zu berücksichtigen, dass die über den Impuls „Geben Sie möglichst konkret an, was Sie gelernt haben.“ unterstellt wird, dass ein Lernzuwachs stattgefunden hat. In Bezug auf das zugrundeliegende Modell der Professionalisierung und die Anlage der Seminare wird im Folgenden in den Blick genommen, (a) welche Facetten der Dispositionen von den Studierenden in welchem Anteil erweitert, (b) welche Teilfacetten von Diagnosekompetenz genannt werden und (c) inwiefern die selbstberichtete Kompetenzentwicklung seminarspezifisch erscheint. [40]

Wissen versus Handlungspotenzial

Aufgrund der selbst durchgeführten Diagnose und diagnosegeleiteten Förderung in den Lehrveranstaltungen ist zu erwarten, dass die Studierenden auf der Ebene der Handlungspotenziale profitiert haben. Die Auswertung in Abbildung 3 zeigt, dass die Studierenden zu etwa gleichen Teilen Aspekte formulierten, die der Ebene der Wissensfacetten (41 % der codierten Aussagen) und den Handlungspotenzialen (42 % der codierten Aussagen) zugeordnet wurden. 11 % der Aussagen thematisierten forschende Selbstreflexionen. Die Ergebnisse weisen damit grob darauf hin, dass die Studierenden einschätzen, sowohl auf der Ebene von Wissen Neues gelernt als auch konkrete Fähigkeiten und Fertigkeiten erworben zu haben. Zudem notierten sie Reflexionen über sich und ihre Rolle als Lehrkraft oder ihren Lernprozess und diesbezügliche Erkenntnisse. Dieser Aspekt ist zwar gemäß dem zugrundeliegenden Modell der Professionalisierung nicht klassisch der Disposition zuzuordnen, wurde hier aber explizit aufgenommen, um deutlich zu machen, dass die Reflexion des eigenen Lernens und die Notwendigkeit des Weiterlernens ein entscheidender Aspekt für die Expertise von Lehrkräften darstellt und die Studierenden im Rahmen der Veranstaltung entsprechende Erfahrungen machen konnten. [41]

Abbildung 3: Überblick über die Codierung (Gesamt)

Während sich im Rahmen von Wissen ungefähr gleich viele Aussagen zu den Bereichen Diagnose (Prinzipien und Methoden der Diagnose (mathematischer) Lernprozesse) und zur Planung von Förderung fanden, können im Bereich der Handlungspotenziale doppelt so viele Aussagen zur Förderung identifiziert werden, wenn die allgemeinen Aussagen zur Förderung (z. B. „Auswahl, Legitimation u. Umsetzung von Unterrichtgegenständen/Fördermaterial“), zur Planung von Förderung („Ich habe gelernt, worauf ich bei der Aufgabenkonstruktion achten muss, um auch den gewünschten Erfolg zu bekommen“) und zur Orchestrierung von Förderung („Flexibler im Umgang mit Fördersituationen werden: Zeitmanagement, spontane Aufgaben einschieben oder weglassen“) zusammengefasst werden. Dies könnte ein Hinweis darauf sein, dass der Zuwachs von Fähigkeiten in der diagnosegeleiteten Förderung von den angehenden Lehrkräften eher dem Bereich der Förderung zugeordnet wurde, während die in der Förderung erfolgte Diagnose entweder nicht so prominent wahrgenommen wurde oder der Kompetenzzuwachs als weniger groß oder weniger entscheidend empfunden wird. Der Anteil der Nennung an Wissenszuwachs im Bereich der mathematikdidaktischen Konzepte, Theorien und Methoden scheint gering zu sein, dabei ist jedoch zu beachten, dass die Studierenden aufgrund der Grundlegung der fach- und fachdidaktischen Konzepte in vorausgegangenen Semestern, vertiefte Kenntnisse möglicherweise als weniger notationswürdig empfinden als neu erworbene Handlungspotentiale. [42]

Diagnose von Lernprozessen

Die Aspekte, die als Diagnose (mathematischer) Lernprozesse die Wissensfacette ausmachen, und von den Studierenden genannt werden, beziehen sich auf [43]

  • Prinzipien und Methoden der Diagnose [44]

  • Kenntnis von (mathematikdidaktischen) Diagnoseinstrumenten, ihrer Charakteristik und Vor- und Nachteilen [45]

  • Trennung zwischen Beobachtung und Deutung [46]

und liegen damit auf den Ebenen der konkreten Anwendung von Diagnosen sowie auf der Ebene der diagnostischen Deutung (vgl. Pott, 2019). Bei den genannten diagnostischen Fähigkeiten und Fertigkeiten, also Handlungspotenzialen, werden Aspekte formuliert, die nach Pott (2019, S. 107) für die Vernetzung von mathematikdidaktischer und sonderpädagogischer Kompetenz bei der diagnostischen Deutung zentral sind: [47]

  • Deutung der Diagnoseergebnisse hinsichtlich der gezeigten mathematischen Kompetenzen [48]

  • Entwicklung von Fördermaßnahmen auf der Grundlage des Wissens aus den gedeuteten mathematischen Fähigkeiten und Schwierigkeiten [49]

Dabei bleiben in den Aussagen der Studierenden die konkreten mathematischen Gegenstände, Aussagen, Vorstellungen oder Fehler – also die spezifischen mathematischen Schwierigkeiten – unerwähnt (vgl. Abb. 3). Insgesamt machen die Angaben zu spezifischen Vorgehensweisen von Lernenden, wozu auch typische Fehler gehören, mit 3 % nur einen sehr kleinen Teil der Angaben aus und lassen sich zudem den von der konkreten Situation recht unabhängig beschriebenen Wissenselementen zuordnen (z. B. „Herangehensweisen zum Erlernen der Subtraktion“). Auch hier ist zu vermuten, dass diese spezifischen mathematischen Konkretisierungen durch die Verortung der Lehrveranstaltungen für die Studierenden als weniger notationswürdig erscheinen. [50]

Besonderheiten der Seminare

Betrachtet man die Einschätzung getrennt nach Seminaren (Abb. 4), so zeigt sich, dass die Anteile der einzelnen Facetten der Disposition zwischen den einzelnen Seminaren durchaus unterschiedlich sind. Dabei ist die Verteilung zwischen den Veranstaltungen LV-B und LV-C ähnlich, obwohl sie an unterschiedlichen Standorten mit Studierenden unterschiedlicher Lehrämter durchgeführt wurden. Auffällig ist, dass in LV-A der Anteil der Aussagen zum Förderschwerpunkt im Vergleich zu den anderen Seminaren deutlicher höher ist. Dies ist vermutlich darin begründet, dass in dieser Veranstaltung Studierende des Lehramts Grundschule explizit aufgefordert wurden, mit einem Kind mit (diagnostiziertem) sonderpädagogischem Unterstützungsbedarf zu arbeiten, was für viele Studierende eine bewusste Erstbegegnung darstellte und entsprechend als bedeutend rückgemeldet wurde. In den Veranstaltungen LV-B und LV-C wurden hingegen Kinder mit Schwierigkeiten beim Mathematiklernen im Heterogenitätsspektrum inklusiver Settings betrachtet, ohne dass eine Statusdiagnose vorlag oder thematisiert wurde. [51]

Abbildung 4: Lehrveranstaltungsspezifische Ergebnisse
Auswertung der geschlossenen Items

Betrachtet man ergänzend die Auswertungen der geschlossenen Items, zeigen sich in allen drei Lehrveranstaltungen bei den ausgewerteten 7 Ankeritems zu den Bereichen Wissen, Handlungspotenziale und Wertorientierungen signifikante Unterschiede und dabei starke bis sehr starke Effekte bei der eigenen Einschätzung der Kompetenzentwicklung. Abbildung 5 und 6 zeigen exemplarisch die Ergebnisse zweier Items, die Entsprechungen der Facetten Wissen und Handlungspotenziale repräsentieren. Abbildung 5 zeigt die Ergebnisse zum Item Wissen (Signifikanz: LV-A: .010; LV-B: .023, LV-C: .000; Effektstärke: LV-A: -0.7114, LV-B: -0.6556, LV-C: -0.8346), Abbildung 6 die Ergebnisse zum entsprechenden Item Handlungspotenzial (Signifikanz: LV-A: .007, LV-B: .002, LV-C: .000; Effektstärke: LV-A: -0.7527, LV-B: -0.8761, LV-C: -0.8714). [52]

Abbildung 5: Ergebnisse Item ‚Wissen’
Abbildung 6: Ergebnisse Item ‚Handlungspotenziale’

In allen drei Lehrveranstaltungen wird der eigene Kompetenzzuwachs bei Wissen und Handlungspotenzialen von den Studierenden hoch eingeschätzt. Insgesamt wird jedoch die final erreichte Kompetenz im Bereich des Wissens (vgl. Abb. 5; nachher) höher eingeschätzt als im Bereich der Handlungspotenziale (vgl. Abb. 6; nachher). Dies könnte einerseits mit herausfordernden Erlebnissen innerhalb der Performanz im Bereich der Handlungsplanung und Handlung in der Situation (vgl. Abb. 1) und damit der Wahrnehmung des eigenen (beginnenden) Professionalisierungsprozesses und des Aufbaus von Handlungspotenzialen erklärt werden. Andererseits könnten entsprechende Wissenselemente als Voraussetzung für erfolgreiches Handeln erlebt werden, und diesbezügliche Erkenntnisse könnten dazu führen, dass entsprechende Kompetenzen in diesem Bereich als höher bzw. gesicherter erlebt werden. Wie bereits oben angemerkt, sind diese Ergebnisse auf Grund der geringen Stichprobe mit aller Vorsicht zu interpretieren. [53]

Diskussion der Ergebnisse

Die Ergebnisse weisen darauf hin, dass die angehenden Lehrkräfte einschätzen, dass sie ihre Kompetenzen bzgl. Diagnose und Förderung erweitern konnten, und zwar sowohl ihr Wissen als auch ihre Handlungspotenziale. Der Einbezug der Praxiserprobungen bzw. konkreter Handlungserfahrungen und entsprechender Reflexionen ermöglicht offensichtlich auch Kompetenzerweiterungen im Bereich der Handlungspotenziale. Dies wäre aber mit fachdidaktischen Lehrveranstaltungen ohne Praxiserprobungen abzugleichen. Die Tatsache, dass es keine klaren Unterschiede zwischen den drei Lehrveranstaltungen gibt, verwundert zwar auf den ersten Blick, kann aber damit erklärt werden, dass die Ausrichtung zwar von verschiedenen Dozent*innen durchgeführt wurden und individuelle Schwerpunkte z. B. bei den mathematischen Inhalten vorgenommen wurden, diese Lehrenden allerdings bei der Grundanlage ihrer praxisbezogenen Veranstaltung durch die gemeinsame Entwicklung der Evaluationsinstrumente kooperierten und in den Veranstaltungen abgestimmte Ziele verfolgten (vgl. Abschnitt 4.2). Die häufige Nennung der Erfahrung mit sonderpädagogischem Förderbedarf in Seminar A zeigt jedoch, dass auch unterschiedlich bedeutsame Erfahrungen erfasst werden konnten (vgl. Abb. 4). [54]

Forschungsmethodisch sind Limitationen in der insgesamt geringen Anzahl der Fragebögen sowie unterschiedlichen Anzahl aus den einzelnen Lehrveranstaltungen zu sehen, was vor allem bei der Gesamtanalyse zu berücksichtigen ist (Abb. 3). Zudem ist die bei den geschlossenen Items als auch bei der Auswertung der offenen Frage vorgenommene Trennung zwischen Wissen und Handlungspotenzialen insofern kritisch zu betrachten, als es sich dabei um ein theoretisches Konstrukt handelt (vgl. Kaiser, Seitz & Slodczyk, 2020). Der sprachlichen Formulierung der Aspekte durch die Studierenden kam bei der Zuordnung zu den Kategorien eine hohe Bedeutung zu, da diese mitentschied, ob eher ein Zuwachs von Wissen oder von Handlungspotenzial beschrieben wurde, was zwar im Sinne der qualitativen Inhaltsanalyse stringent vorgenommen war, aber forschungsmethodisch zu berücksichtigen ist. Gleichwohl bestätigen und erweitern die Ergebnisse die Befunde von Philipp (2018) und Heinrichs (2015) im Lehramt Grundschule bzw. Sonderpädagogische Förderung. In den weiteren Auswertungen wird zu prüfen sein, welche lernförderlichen Aktivitäten die Studierenden welchen weiteren erreichten Lernzielen zuschreiben, d. h. worauf sie ihren Kompetenzerwerb zurückführen (vgl. auch Scherer, 2022). Offen bleibt darüber hinaus, ob sich der selbsteingeschätzte Kompetenzerwerb auch in einer Fremdeinschätzung bestätigen lässt. [55]

Das hier genutzte Professionalisierungsmodell ist in weiteren Studien bezüglich der fachbezogenen Diagnose und Förderung (im inklusiven Mathematikunterricht) genauer zu diskutieren. Die fehlende fachbezogene Fassung von Diagnose und Förderung im genutzten Modell führte zu einer eigenen Ausdifferenzierung von Wissensfacetten und Handlungspotentialen, da Diagnose und Förderung bezogen auf das fachliche Lernen nicht gegenstandsfrei gedacht werden können. [56]

Perspektiven

Kompetenzen hinsichtlich diagnosegeleiteter Förderung sind für die inklusionsbezogene Gestaltung von Unterricht zentral, und ein solcher Kompetenzerwerb muss im Studium durch entsprechende, insbesondere auch fachbezogene, Lehrveranstaltungen ermöglicht werden. Dabei können nicht nur Kompetenzen im Bereich des Wissens, sondern auch Handlungspotenziale erworben werden, wenn Lehrveranstaltungen auf eine Vernetzung von Theorie und Praxis setzen und diese exemplarisch erfahrbar machen. Die Studierenden haben dann die Möglichkeit, bereits in der ersten Phase der Lehrer*innenbildung den Professionalisierungsprozess zu durchlaufen. Dabei erscheint wichtig, dass sie diesen mitunter auch als krisenhaft erleben, z. B. wenn geplante Förderangebote nicht im intendierten Sinne zu erfolgreichen Lernprozessen führen oder trotz einer erfolgten Diagnose viele Fragen offen bleiben, denn gerade das krisenhafte Erleben zeichnet die Professionalisierung von Lehrkräften aus (vgl. Helsper, 2014). Um Expertise hinsichtlich der Diagnose und Förderung mathematischer Lernprozesse zu erlangen, ist entsprechendes Wissen mit Handlungserfahrungen zu verbinden und zu reflektieren. Möglicherweise sollte dabei auch die Reflexion der Vertiefung und Anwendung von bereits erworbenen fachlichen und fachdidaktischen Kenntnissen im Kontext der Handlungserfahrung in inklusiven Settings gezielt angeregt werden. So können mögliche Spannungsfelder und ein produktiver Umgang mit ihnen schon in der ersten Phase der Lehrer*innenbildung diskutiert werden. [57]

1Gefördert als Lehrinnovationund angebunden an ein Kooperationsprojekt der Universitäten Duisburg-Essen und Paderborn (https://www.stifterverband.org/lehrfellowships/2017/haesel-weide_scherer; vgl. auch Del Piero et al., 2019).↩
2Ein/e Student*in aus LV-A hat diese Frage nicht beantwortet.↩

Literatur

  1. Baumert, J. & Kunter, M. (2006). Stichwort: Professionelle Kompetenz von Lehrkräften. Zeitschrift für Erziehungswissenschaft, 9(4), 469–520. doi: 10.1007/s11618-006-0165-2.
  2. Del Piero, N., Hähn, K., Häsel-Weide, U., Kindt, C., Rütten, C., Scherer, P. & Weskamp, S. (2019). Teacher students' competence acquisition in teaching-learning-labs. In J. Novotná & H. Moraová (Hrsg.), SEMT 2019. International Symposium Elementary Maths Teaching. August 18-23, 2019. Proceedings: Opportunities in Learning and Teaching Elementary Mathematics (S. 469–471). Prague: Charles University, Faculty of Education.
  3. Filipiak, A. (2020). Kompetenzmodellierung in inklusionsorientierter LehrerInnenbildung. Konstruktion eines kompetenzorientierten Lehrkonzepts zur Entwicklung und Förderung (multiprofessioneller) Kooperationsfähigkeit und -bereitschaft bei Lehramtsstudierenden. QfI -- Qualifizierung für Inklusion, 2(1). doi: 10.21248/QfI.21.
  4. Fröhlich-Gildhoff, K., Nentwig-Gesemann, I. & Pietsch, S. (2011). Kompetenzorientierung in der Qualifizierung frühpädagogischer Fachkräfte. Expertise der Weiterbildungsinitiative Frühpädagogische Fachkräfte (WiFF)(19). München: DJI.
  5. Fröhlich-Gildhoff, K., Weltzien, D., Kirstein, N., Pietsch, S. & Rauh, K. (2014). Kompetenzen früh-/kindheitspädagogischer Fachkräfte im Spannungsfeld von normativen Vorgaben und Praxis. Freiburg: Zentrum für Kinder- und Jugendforschung. Abgerufen unter: https://www.bmfsfj.de/resource/blob/94174/6a47780ac348d80e4718f38d52230ae8/kompetenzen-frueh-kindheitspaedagogischer-fachkraefte-im-spannungsfeld-von-normativen-vorgaben-und-praxis-data.pdf.
  6. Geisen, M. (2021). Grund- und Förderschullehrpersonen im inklusiven Mathematikunterricht. Eine videovignettenbasierte Untersuchung förderdiagnostischer Kompetenzen am Beispiel des Sachrechnens. Wiesbaden: Springer.
  7. Götze, D. & Hang, E. (2017). Mathematische Sprache und Ausdruck. Chancen und Möglichkeiten eines sprachaktivierenden und -fördernden Mathematikunterrichts. In U. Häsel-Weide & M. Nührenbörger (Hrsg.), Gemeinsam Mathematik lernen -- mit allen Kindern rechnen (S. 68–77). Frankfurt am Main: Grundschulverband e. V..
  8. Hartig, J. & Jude, N. (2007). Empirische Erfassung von Kompetenzen und psychometrische Kompetenzmodelle. In Bundesministerium für Bildung und Forschung (Hrsg.), Möglichkeiten und Voraussetzungen technologiebasierter Kompetenzdiagnostik (S. 17–36). Bonn: BMBF.
  9. Häsel-Weide, U. & Nührenbörger, M. (2012). Fördern im Mathematikunterricht. In H. Bartnitzky, U. Hecker & M. Lassek (Hrsg.), Individuell fördern -- Kompetenzen stärken in der Eingangsstufe (Kl. 1 und 2) (S. 170–210). Frankfurt am Main: Grundschulverband e.V..
  10. Häsel-Weide, U. & Nührenbörger, M. (2017). Das Zahlenbuch. Förderkommentar Lernen zum 1. Schuljahr. Leipzig: Klett.
  11. Häsel-Weide, U., Nührenbörger, M., Moser Opitz, E. & Wittich, C. (2019). Ablösung vom zählenden Rechnen. Fördereinheiten für heterogene Lerngruppen (5. Auflage). Seelze: Klett Kallmeyer.
  12. Häsel-Weide, U. & Prediger, S. (2017). Förderung und Diagnose im Mathematikunterricht -- Begriffe, Planungsfragen und Ansätze. In M. Abshagen, B. Barzel, J. Kramer, T. Riecke-Baulecke, B. Rösken-Winter & C. Selter (Hrsg.), Basiswissen Lehrerbildung: Mathematik unterrichten (S. 167–181). Seelze: Kallmeyer/Klett.
  13. Häsel-Weide, U., Seitz, S., Wallner, M., Wilke, Y. & Heckmann, L. (2021). Mit Aufgaben im inklusiven Mathematikunterricht professionell umgehen -- Erkenntnisse einer Interviewstudie mit Lehrpersonen der Sekundarstufe. QfI -- Qualifizierung für Inklusion, 3(1). doi: 10.21248/qfi.57.
  14. Heinrichs, H. (2015). Diagnostische Kompetenz von Mathematik-Lehramtsstudierenden. Messung und Förderung. Wiesbaden: Springer Spektrum. doi: 10.1007/978-3-658-09890-2.
  15. Helsper, W. (2014). Lehrerprofessionalität -- der strukturtheoretische Professionsansatz zum Lehrerberuf. In E. Terhart, H. Bennewitz & M. Rothland (Hrsg.), Handbuch der Forschung zum Lehrerberuf (S. 216–240). Münster and New York: Waxmann.
  16. Hess, B. & Nührenbörger, M. (2017). Produktives Fördern im inklusiven Mathematikunterricht. In U. Häsel-Weide & M. Nührenbörger (Hrsg.), Gemeinsam Mathematik lernen -- mit allen Kindern rechnen (S. 275–287). Frankfurt am Main: Grundschulverband e. V..
  17. Hoth, J. (2016). Situationsbezogene Diagnosekompetenz von Mathematiklehrkräften. Eine Vertiefungsstudie zur TEDS-Follow-Up-Studie. Wiesbaden: Springer Spektrum. doi: 10.1007/978-3-658-13156-2.
  18. Hoth, J., Döhrmann, M., Kaiser, G., Busse, A., König, J. & Blömeke, S. (2016). Diagnostic competence of primary school mathematics teachers during classroom situations. ZDM Mathematics Education, 48(1-2), 41–53. doi: 10.1007/s11858-016-0759-y.
  19. Kaiser, M., Seitz, S. & Slodczyk, N. (2020). Expertise als übergreifendes Paradigma der Professionalisierungsforschung zur inklusionsbezogenen Fortbildung von Lehrpersonen. QfI -- Qualifizierung für Inklusion, 2(1). doi: 10.21248/qfi.30.
  20. Krummheuer, G. & Fetzer, M. (2010). Der Alltag im Mathematikunterricht. Beobachten -- Verstehen -- Gestalten. Heidelberg: Spektrum.
  21. Kultusministerkonferenz (2015). Lehrerbildung für eine Schule der Vielfalt. Gemeinsame Empfehlung von Hochschulrektorenkonferenz und Kultusministerkonferenz (Beschluss der Kultusministerkonferenz vom 12.03.2015/Beschluss der Hochschulrektorenkonferenz vom 18.03.2015). Abgerufen unter: http://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2015/2015_03_12-Schule-der-Vielfalt.pdf.
  22. Kultusministerkonferenz (2019). Ländergemeinsame inhaltliche Anforderungen für die Fachwissenschaften und Fachdidaktiken in der Lehrerbildung. Beschluss d. KMK v. 16.10.2008 i. d. F. v. 16.05.2019. Abgerufen unter: https://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2008/2008_10_16-Fachprofile-Lehrerbildung.pdf.
  23. Leuders, T., Dörfler, T., Leuders, J. & Phillip, K. (2018). Diagnostic Competence of Mathematics Teachers: Unpacking a Complex Construct. In T. Leuders, K. Philipp & J. Leuders (Hrsg.), Diagnostic Competence of Mathematics Teachers Unpacking a Complex Construct in Teacher Education and Teacher Practice (S. 3–31). Cham: Springer.
  24. Mayring, P. (2010). Qualitative Inhaltsanalyse. Grundlagen und Techniken. Weinheim and Basel: Beltz.
  25. Ministerium für Schule und Weiterbildung (2020). Gesetz über die Ausbildung für Lehrämter an öffentlichen Schulen (Lehrerausbildungsgesetz -- LABG). Abgerufen unter: https://bass.schul-welt.de/9767.htm#1-8p2.
  26. Misoch, S. (2015). Qualitative Interviews. Berlin and München and Boston: de Gruyter.
  27. Moser Opitz, E. (2006). Förderdiagnostik: Entstehung -- Ziele -- Leitlinien -- Beispiele. In M. Grüßing & A. Peter-Koop (Hrsg.), Die Entwicklung mathematischen Denkens in Kindergarten und Grundschule. Beobachten -- Fördern -- Dokumentieren (S. 10–28). Offenbach: Mildenberger.
  28. Moser Opitz, E. (2010). Diagnose und Förderung: Aufgaben und Herausforderungen für die Mathematikdidaktik und die mathematikdidaktische Forschung. In A. Lindmeier & S. Ufer (Hrsg.), Beiträge zum Mathematikunterricht 2010 (S. 11–18). Münster: WTM. doi: 10.5167/uzh-40288.
  29. Moser Opitz, E. & Nührenbörger, M. (2015). Diagnostik und Leistungsbeurteilung. In R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme & H.-G. Weigand (Hrsg.), Handbuch der Mathematikdidaktik (S. 489–510). Heidelberg: Springer. doi: 10.1007/978-3-642-35119-8.
  30. Philipp, K. (2018). Diagnostic Competences of Mathematics Teachers with a View to Processes and Knowledge Resources. In T. Leuders, K. Philipp & J. Leuders (Hrsg.), Diagnostic Competence of Mathematics Teachers Unpacking a Complex Construct in Teacher Education and Teacher Practice (S. 109–127). Cham: Springer.
  31. Pott, A. (2019). Diagnostische Deutungen im Lernbereich Mathematik. Diagnostische Kompetenzen von Lehramtsstudierenden für sonderpädagogische Förderung und den Primarbereich. Wiesbaden: Springer. doi: 10.1007/978-3-658-24871-0.
  32. Reinhold, S. (2018). Revealing and Promoting Pre-service Teachers' Diagnostic Strategies in Mathematical Interviews with First-Graders. In T. Leuders, K. Philipp & J. Leuders (Hrsg.), Diagnostic Competence of Mathematics Teachers Unpacking a Complex Construct in Teacher Education and Teacher Practice (S. 129–148). Cham: Springer.
  33. Reis, O. & Seitz, S. (2019). Inklusionsbezogene Qualifizierung im Lehramtsstudium. Markt-PLAZ 39. Abgerufen unter: https://plaz.uni-paderborn.de/fileadmin/plaz/Fort-_und_Weiterbildungsangebote/Markt-PLAZ/MP-Heft39-SoSe-19.pdf.
  34. Rottmann, T., Wellensiek, N. & Lüken, M. M. (2018). Diagnose mathematischer Kompetenzen als Gegenstand Forschenden Lernens im Praxissemester. HLZ, 1(1), 331–344. doi: 10.4119/UNIBI/hlz-73.
  35. Schäfer, H. & Rittmeyer, C. (Hrsg.). (2015). Handbuch Inklusive Diagnostik. Weinheim: Beltz.
  36. Scherer, P. (2020). Low achievers in mathematics -- Ideas from the Netherlands for developing a competence-oriented view. In M. van den Heuvel-Panhuizen (Hrsg.), International Reflections on the Netherlands Didactics of Mathematics -- Visions on and Experiences with Realistic Mathematics Education (S. 113–132). Cham: Springer.
  37. Scherer, P. (2022). Umgang mit Vielfalt im Mathematikunterricht der Grundschule -- Welche Kompetenzen sollten Lehramtsstudierende erwerben?. In K. Eilerts, R. Möller & T. Huhmann (Hrsg.), Auf dem Weg zum neuen Mathematiklehren und -lernen 2.0 (S. 11–25). Wiesbaden: Springer. doi: 10.1007/978-3-658-33450-5_2.
  38. Schiefele, C., Streit, C. & Sturm, T. (2019). Pädagogische Diagnostik und Differenzierung in der Grundschule. Mathe und Deutsch inklusiv unterrichten. München: Ernst Reinhard Verlag.
  39. Schulz, A. (2014). Fachdidaktisches Wissen von Grundschullehrkräften. Diagnose und Förderung bei besonderen Problemen beim Rechnenlernen. Wiesbaden: Springer. doi: 10.1007/978-3-658-08693-0.
  40. Selter, C. (2017). Förderorientierte Diagnose und diagnosegeleitete Förderung. In A. Fritz, S. Schmidt & G. Ricken (Hrsg.), Handbuch Rechenschwäche. Lernwege, Schwierigkeiten und Hilfen bei Dyskalkulie (S. 375–394). Weinheim: Beltz.
  41. Terhart, E. (2000). Perspektiven der Lehrerbildung in Deutschland. Abschlussbericht der von der Kultusministerkonferenz eingesetzten Kommission. Weinheim: Beltz.
  42. Terhart, E. (2011). Lehrerberuf und Professionalität. Gewandeltes Begriffsverständnis -- neue Herausforderungen. In W. Helsper & R. Tippelt (Hrsg.), Pädagogische Professionalität (Zeitschrift für Pädagogik: Beiheft, Bd. 57) (S. 202–224). Weinheim: Beltz. doi: 10.25656/01:7095.
  43. Wember, F. B. (1998). Zweimal Dialektik: Diagnose und Intervention, Wissen und Intuition. Sonderpädagogik, 28(2), 108–120.

Kontakt:

Kristina Hähn, Pädagogische Hochschule der FH Nordwestschweiz, Professur Mathematikdidaktik und mathematisches Denken im Kindesalter, Hofackerstr. 30, CH-4132 Muttenz
E-Mail: kristina.haehn@fhnw.ch

Zitation:

Hähn, K., Häsel-Weide, U. & Scherer, P. (2022). Diagnosegeleitete Förderung im inklusiven Mathematikunterricht der Grundschule – Professionalisierung durch reflektierte Handlungspraxis in der Lehrer*innenbildung. QfI - Qualifizierung für Inklusion, 3(2), doi:

Eingereicht:

15.04.2021