Gemeinsame Lernumgebungen entwickeln (GLUE), ein Blended-Learning Fortbildungskonzept für den inklusiven Mathematikunterricht
Developing collaborative learning environments, a blended learning training concept for inclusive mathematics teaching
DOI:
https://doi.org/10.21248/qfi.7Schlagworte/Keywords
Blended-Learning, Lehrerfortbildung, Inklusiver Unterricht, Gemeinsames Lernen, Professionalisierung, Mathematik, Blended learning, teachers’ in-service training, inclusive teaching, collaborative learning, professionalization, mathematics instructionZusammenfassung
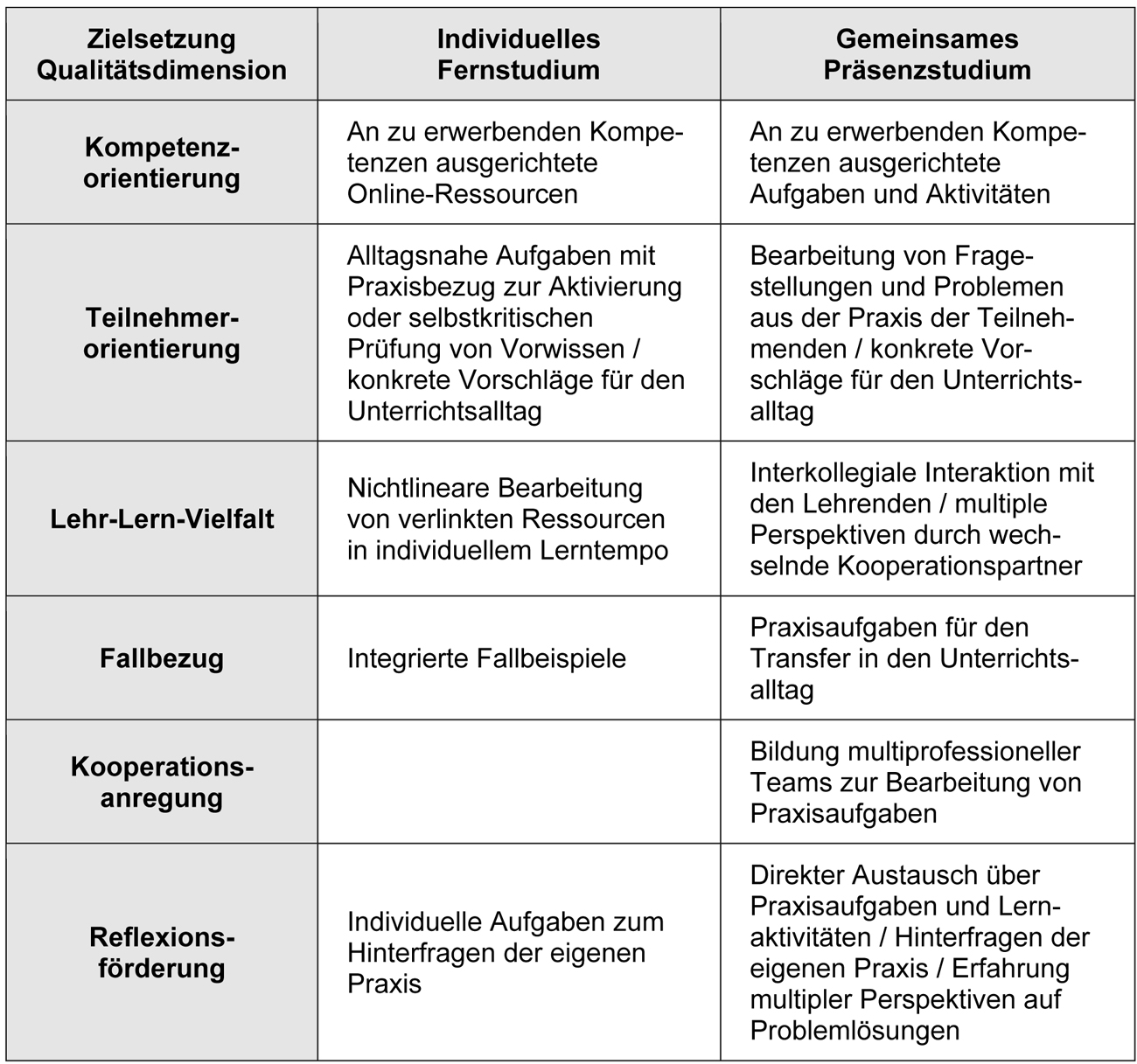
Der vorliegende Beitrag beschreibt den theoretischen Hintergrund und das Design des Projekts GLUE (Gemeinsame Lern-Umgebungen Entwickeln). Die Konzeption der Gemeinsamen Lern-Umgebungen zielt im Sinne der Prinzipien des ‚Universal Design of Learning‘ (Hall, Meyer & Rose, 2012) darauf ab, den inklusiven Mathematikunterricht von einem gemeinsamen Lerngegenstand aus zu denken, der einerseits Zugänglichkeit für alle Lernenden schafft und andererseits Unterstützungsmaßnahmen auf unterschiedlichen Niveaustufen zulässt.
Das Projekt geht der Frage nach, wie sich die Kompetenzentwicklung von berufserfahrenen Lehrkräften der allgemeinen Schule und für sonderpädagogische Förderung durch Fortbildungsangebote zum inklusiven Mathematikunterricht wirksam unterstützen lässt. Hierzu wurde ein Blended-Learning-Angebot zur Entwicklung gemeinsamer Lernumgebungen für alle Kinder einer Lerngruppe erarbeitet, die sich auch von mehreren Lehrkräften gemeinsam entwickeln lassen.
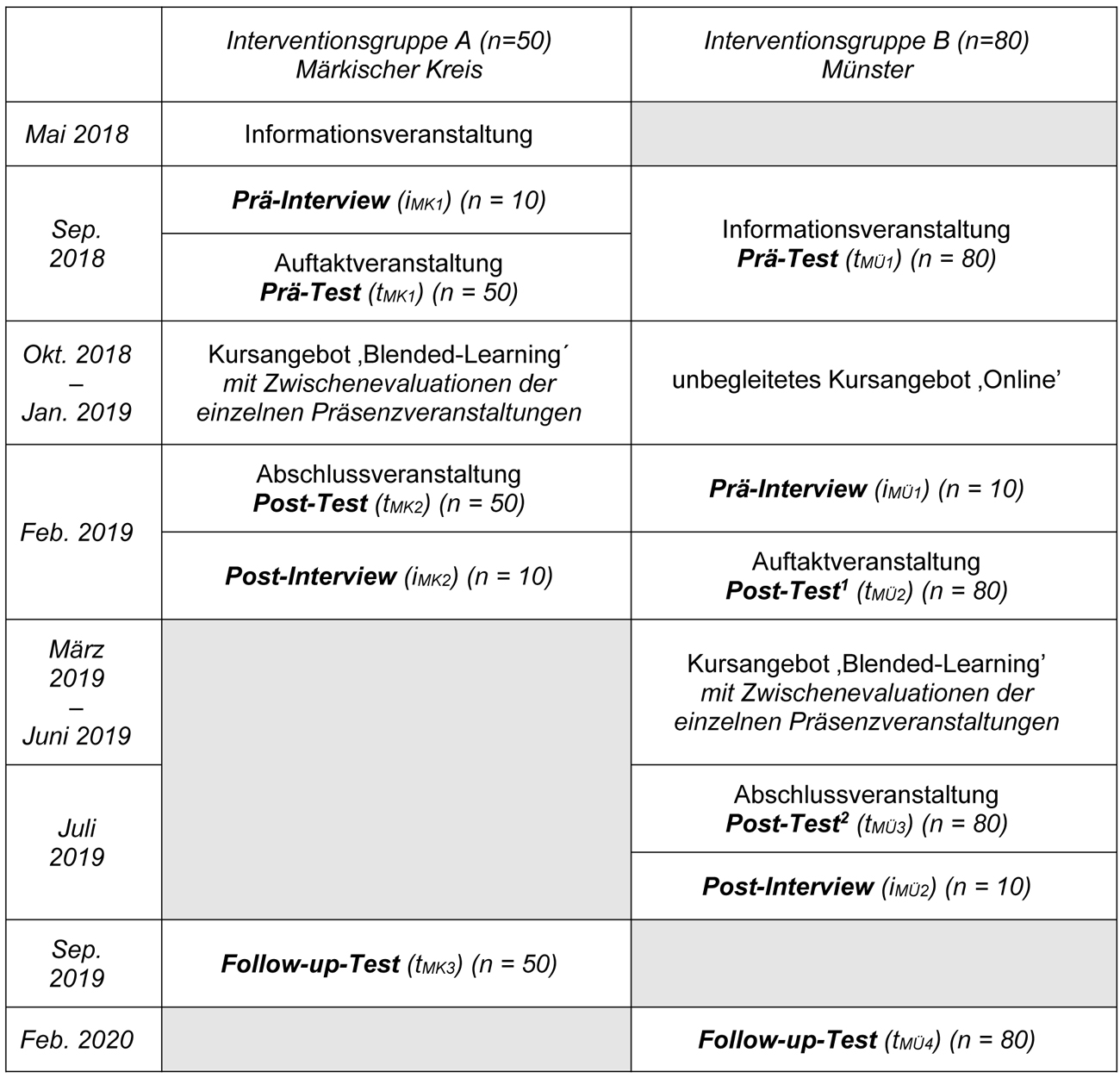
In diesem Beitrag werden der theoretische Hintergrund, die Konzeption und die methodische Anlage des Projekts vorgestellt. Kapitel 1 befasst sich mit Differenzieren und Fördern im Mathematikunterricht der Primarstufe, Kapitel 2 diskutiert zentrale Befunde zur Wirksamkeit von Lehrerfortbildungsmaßnahmen sowie zu Blended-Learning-Angeboten. Im dritten Kapitel werden auf dieser Grundlage die Ziele des Projekts (Kap. 3.1), die Inhalte und die Struktur des Fortbildungsangebots (Kap., 3.2), die Forschungsfragen (Kap. 3.3) und das Design der Interventionsstudie dargestellt (Kap. 3.4). Die Wirksamkeit wird in einem ausbalancierten Prä-Post-Follow-Up-Test-Design im Vergleich zu unbegleiteten Online-Angeboten evaluiert, die Ergebnisse sollen in einer Folgepublikation kommuniziert werden.
Abstract
This paper describes the theoretical background and the design of the GLUE project (Gemeinsame Lern-Umgebungen Entwickeln; Developing Collaborative Learning Environments). In line with the principles of ‚Universal Design of Learning‘ (Hall, Meyer & Rose, 2012), the GLUE conception aims to base inclusive mathematics education - wherever appropriate - on common topics. This approach provides accessibility for all learners on the one hand and allows support measures at different levels on the other.
The project addresses the question of how the development of competence of experienced teachers of different professions can be effectively supported by inservice education courses for inclusive mathematics education. For this purpose, a blended learning course on the design of collaborative learning environments has been developed.
In this article, the theoretical background and the research design of the project will be presented. Section 1 will discuss the topics of differentiation and promotion in primary school mathematics education. Section 2 will introduce key findings on the effectiveness of teacher training and blended learning services. In the third chapter, the objectives of the project (Section 3.1), the content and structure of the inservice course (Section 3.2), the research questions (Section 3.3) and the design of the intervention study will be presented (Section 3.4). The effectiveness shall be evaluated in a balanced pre-post follow-up test design by comparison with unaccompanied online offers in an investigation to be reported on in a future publication.