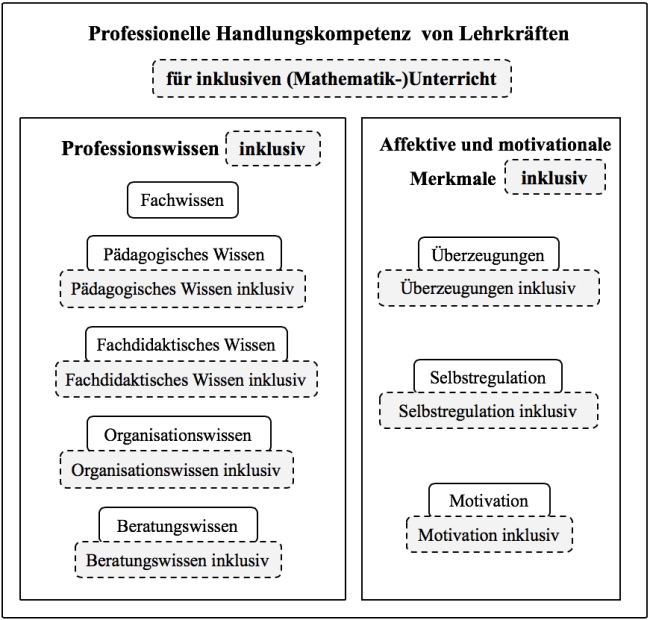
Ansatz zur Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht. Identifizierte Kompetenzbereiche bei Lehrkräften zu Beginn einer Fortbildung

Approach to Further Develop the Model of Teachers’ Professional Competence for Inclusive (Mathematics) Teaching – Identified Teachers’ Domains of Competence at the Beginning of a Professional Development Program

Autor/innen

  • Jennifer Bertram Ruhr-Universität Bochum
  • Natascha Albersmann Ruhr-Universität Bochum
  • Katrin Rolka Ruhr-Universität Bochum

DOI:

https://doi.org/10.21248/qfi.25

Schlagworte/Keywords

Professionelle Handlungskompetenz, Inklusion, Mathematikunterricht, Lehrerfortbildung, Professional competence, Inclusion, Mathematics teaching, Professional development program

Zusammenfassung

Ausgehend von spezifischen Anforderungen inklusiver Settings wird in diesem Beitrag ein Ansatz zur Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht vorgestellt. Inklusion wird dabei verstanden als fachliches Lernen und gemeinsame Teilhabe aller Schülerinnen und Schüler. Für die Weiterentwicklung werden zunächst Anforderungen durch inklusive Bildung betrachtet, einerseits abgeleitet aus verschiedenen Aufgaben- und Kompetenzkatalogen, andererseits basierend auf Kernbeständen für den Umgang mit Heterogenität im (Mathematik-)Unterricht im Allgemeinen und für inklusiven (Mathematik-)Unterricht im Speziellen. Anschließend wird daraus Wissen zur Bewältigung dieser Anforderungen abgeleitet und unter Rückgriff auf die verschiedenen Bereiche des Professionswissens (Fachwissen, pädagogisches Wissen, fachdidaktisches Wissen, Organisationswissen und Beratungswissen) weiter ausgeführt, wobei der Fokus auf das fachdidaktische Wissen im inklusiven Mathematikunterricht gelegt wird. Die affektiven und motivationalen Merkmale (Überzeugungen, Selbstregulation und Motivation) der professionellen Handlungkompetenz werden ebenfalls in die Weiterentwicklung des Modells einbezogen. Insgesamt erfolgt die Weiterentwicklung des Modells somit im Rahmen einer Erweiterung der einzelnen bestehenden Kompetenzbereiche um Aspekte, die unter Inklusionsgesichtspunkten besondere Bedeutung erfahren. Mit der Identifizierung von Kompetenzbereichen bei Lehrkräften zu Beginn einer Fortbildung zu inklusivem Mathematikunterricht wird ein Beispiel präsentiert, wie das weiterentwickelte Modell angewendet werden kann. In diesem Zusammenhang konnten in den Äußerungen der Lehrkräfte – abgesehen vom Fachwissen – alle Kompetenzbereiche identifiziert werden. Abschließend werden Möglichkeiten vorgestellt, wie das Modell im Kontext der Lehrerprofessionalisierungsforschung weiterhin eingesetzt werden kann.

Abstract

Based on specific requirements by inclusive settings, this paper presents an approach to further develop the model of teachers’ professional competence for inclusive (mathematics) teaching. For this, inclusion is meant to be subject-specific learning and joint participation of all pupils. First, requirements by inclusive education are considered. They are both derived from various task and competence catalogues as well as based on core elements for dealing with heterogeneity in (mathematics) classrooms in general and for inclusive (mathematics) teaching in particular. From this, knowledge for coping with these requirements is derived and explicated relying on the domains of professional knowledge (content knowledge, pedagogical knowledge, pedagogical content knowledge, organizational knowledge and counseling knowledge), whereby the pedagogical content knowledge for inclusive mathematics teaching is in focus. Affective and motivational characteristics (beliefs, self-regulation and motivation) of the professional competence are also included. Overall, the further development of the model is realized through an extension of the domains of competence by including aspects that are of particular importance from an inclusive perspective. By identifying teachers’ domains of competence at the beginning of a professional development program on inclusive mathematics teaching, an example is given of how the further developed model can be applied. In this context, all domains of competence – except content knowledge – could be identified within the teachers’ statements. Finally, more possibilities of how the model can be used in further research on teachers’ professional development are presented.

Downloads

Veröffentlicht

2020-07-23

Ausgabe

Bd. 2 Nr. 1 (2020): Pädagogische Fachlichkeit

Rubrik

Artikel

Einleitung

Ziel dieses Beitrags ist eine Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht. Inklusion verstehen wir dabei als fachliches Lernen und gemeinsame Teilhabe aller Schülerinnen und Schüler. Ausgehend von dem Gedanken, dass einerseits keine gesonderte inklusive Didaktik notwendig ist (Korff, 2016) und andererseits für guten inklusiven (Mathematik-)Unterricht zu den Merkmalen guten (Mathematik-)Unterrichts indes weitere Merkmale guten gemeinsamen (Mathematik-)Unterrichts hinzukommen (Klemm & Preuss-Lausitz, 2011), erscheint eine Erweiterung und damit eine Weiterentwicklung des vorhandenen Modells von Baumert und Kunter (2006) ein vielversprechender Ansatz zu sein. [1]

Bisher finden sich vor allem Arbeiten, die einzelne Bereiche der professionellen Handlungskompetenz näher untersuchen. König, Gerhard, Kaspar und Melzer (2019) untersuchen zum Beispiel das pädagogische Wissen für inklusiven Unterricht. Um sowohl alle Wissensbereiche der Unterrichtsebene (Fachwissen, pädagogisches Wissen, fachdidaktisches Wissen) als auch die Schulebene (Organisationswissen, Beratungswissen) zu berücksichtigen, betrachten wir das gesamte Professionswissen. Vor dem Hintergrund, dass professionelle Handlungskompetenz aus einem Zusammenspiel von Professionswissen, Überzeugungen, motivationalen Orientierungen und selbstregulativen Fähigkeiten entsteht (Baumert & Kunter, 2006), verstehen wir professionelle Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht ebenfalls als ein Zusammenspiel der entsprechend erweiterten Kompetenzbereiche. In diesem Zusammenhang fokussiert der vorliegende Beitrag das fachdidaktische Wissen für inklusiven Mathematikunterricht, denn König et al. (2019) halten fest, dass vor allem bisherige Konzeptionen zum pädagogischen und zum fachdidaktischen Wissen „angesichts erweiterter Anforderungen, die im Rahmen neuer Aufgaben im inklusiven Unterricht an Regelschullehrkräfte gestellt werden, zu kurz greifen“ (S. 50). In diesem Zusammenhang werden sowohl Überlegungen zum Umgang mit Heterogenität als auch Ausführungen im Sinne eines inklusiven Mathematikunterrichts herangezogen (vgl. Häsel-Weide & Nührenbörger, 2017; Knipping, Korff, & Prediger, 2017). [2]

Zunächst erfolgt eine Beschreibung von Anforderungen durch inklusive Bildung (Kap. 2.1), um vor diesem Hintergrund die einzelnen erweiterten Kompetenzbereiche detailliert zu betrachten (Kap. 2.2 & 2.3). Im Kontext der Identifikation von Kompetenzbereichen bei Lehrkräften zu Beginn einer Fortbildung wird vorgestellt, wie das Modell beispielhaft angewendet werden kann (Kap. 3). Der Fokus auf einen Fortbildungsrahmen liegt darin begründet, dass sich positive Effekte von Fortbildungsteilnahmen mit Blick auf die Erweiterung der Lehrkompetenzen für inklusive Settings erkennen lassen (z.B. Seifried, 2015). Es wird diesbezüglich dargestellt, inwiefern das erweiterte Modell genutzt werden kann, um Äußerungen von Lehrkräften zur Gestaltung ihres inklusiven Mathematikunterrichts und zur Motivation ihrer Fortbildungsteilnahme zu kategorisieren. Das Ziel der Erweiterung und damit eine Weiterentwicklung des vorhandenen Modells von Baumert und Kunter für inklusiven (Mathematik-)Unterricht geht dementsprechend in diesem Beitrag damit einher, die Tragfähigkeit der Erweiterung im Sinne eines Anwendungsbeispiels zu diskutieren. Abschließend erfolgt ein kurzer Ausblick auf Ideen, wie die Kategorisierung und das erweiterte Modell sowohl für die Fortbildungsgestaltung als auch innerhalb der Forschung genutzt werden können (Kap. 4). [3]

Professionelle Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht

In diesem Kapitel stehen ausgehend vom Modell der professionellen Handlungskompetenz die Konzeptualisierung der einzelnen Kompetenzbereiche für inklusiven Unterricht und mathematikdidaktische Überlegungen im Vordergrund. Den Ausgangspunkt bilden erweiterte Anforderungen an Lehrkräfte, die sich durch Inklusion ergeben, sowie Ausführungen dazu, welche Kompetenzen Lehrkräfte benötigen, um diese Anforderungen bewältigen zu können. [4]

Anforderungen durch Inklusion und Kompetenzen zur Bewältigung

Eine Möglichkeit für die Betrachtung der Anforderungen durch Inklusion ist die Sichtung verschiedener Aufgaben- und Kompetenzkataloge. Auf der Grundlage eines Reviews internationaler Studien leiten Melzer, Hillenbrand, Sprenger und Hennemann (2015) beispielsweise Aufgaben in inklusiven Bildungssystemen sowohl von Lehrkräften der allgemeinen Schulen als auch von sonderpädagogischen Lehrkräften ab. Dahingegen spezifizieren Weiß, Muckenthaler, Heimlich, Küchler und Kiel (2019) Anforderungen an Lehrkräfte ausgehend vom Schulkonzept Inklusion. Als Reaktion auf diese Aufgaben und Anforderungen sind erweiterte Kompetenzen auf Seiten der Lehrkräfte erforderlich (vgl. König et al., 2019). Aktuelle Arbeiten fokussieren dabei die Entwicklung von Kompetenzstrukturmodellen für sonderpädagogische Lehrkräfte (Moser & Kropp, 2014) oder nutzen das Konzept der adaptiven Lehrkompetenz und passen verschiedene Kompetenzbereiche für den Umgang mit Heterogenität in inklusiven Settings an (Fischer, Kopmann, Rott, Veber, & Zeinz, 2014). Teilweise erfolgt eine Verortung im Modell von Baumert und Kunter mit einer anschließenden Fokussierung einzelner Kompetenzbereiche für inklusiven Unterricht (z.B. für sachunterrichtsdidaktisches Wissen: Mester, 2019). Die Arbeiten von König et al. (insbesondere König et al., 2017 sowie König et al., 2019) kombinieren Ergebnisse aus der Sichtung verschiedener Aufgaben- und Kompetenzkataloge mit einer Verortung im Modell von Baumert und Kunter zur Beschreibung professioneller Handlungskompetenz und dessen Erweiterung vor dem Hintergrund inklusiven Unterrichts, sodass wir dieser Vorgehensweise folgen. Des Weiteren sind diese Überlegungen anschlussfähig an bereits identifizierte zentrale Handlungsfelder inklusiver Bildung (z.B. an die Kompetenzbereiche Didaktik, fachliches und fachdidaktisches Wissen, Diagnostik, Attitudes und Beliefs, Individualisierung und Leistungsdifferenzierung, Lehrerkooperation, Beratung und Schulentwicklung; Heinrich, Urban, & Werning, 2013). [5]

Im Kontext der Aufgaben- und Kompetenzkataloge wird auf theoretisch erstellte Anforderungsbeschreibungen und einzelne empirische Untersuchungen zu den von Lehrkräften zu erfüllenden Aufgaben Bezug genommen (Vorgehensweise bei König et al., 2017; König et al., 2019). Daraus werden vier Anforderungsbereiche abgeleitet: Diagnose, Intervention, Management und Organisation sowie Beratung und Kommunikation (König et al., 2019). Den Autorinnen und Autoren zufolge geht es im Bereich Diagnose vor allem um die Diagnostik von Förderbedarfen. Unter Intervention werden Anforderungen gebündelt, die mit didaktisch-methodischen Maßnahmen einhergehen, wie zum Beispiel Individualisierung, sowie Überlegungen zur Klassenführung und zur Strukturierung des Unterrichts. Der Bereich Management und Organisation umfasst eine Kooperation mit jeglichen Partnern, etwa die Zusammenarbeit von Regelschullehrkraft und sonderpädagogischer Lehrkraft. Der Bereich Beratung und Kommunikation wird von König et al. als Anforderungsbereich ausgewiesen, aber nicht näher erläutert. Diese Betrachtungsweise von Anforderungen durch Inklusion bezieht sich innerhalb der Bereiche Diagnose und Intervention auf die Unterrichtsebene und innerhalb der Bereiche Management und Organisation sowie Beratung und Kommunikation auf eine systemische (über den Unterricht hinausgehende) Ebene (König et al., 2019). Es werden somit verschiedene Aufgaben- und Kompetenzkataloge gebündelt, um Anforderungen durch Inklusion abzuleiten, auch wenn die dabei betrachteten Kompetenzkataloge oftmals wenig konkret sind (König et al., 2019), sodass wir zur Spezifizierung der Anforderungen durch inklusive Bildung folgende Überlegungen hinzuziehen. [6]

Einen Schwerpunkt auf die Planung und Gestaltung von Fachunterricht sowie auf Grundideen der fachdidaktischen Orientierung legen Knipping et al. (2017) in ihrem Versuch einer curricularen Bestimmung mathematikdidaktischer Kernbestände für den Umgang mit Heterogenität, wobei sie an einzelnen Stellen explizit inklusiven Mathematikunterricht fokussieren. Knipping et al. (2017) betrachten zunächst drei Aspekte für die Planung und Gestaltung von Fachunterricht, die sie unabhängig vom Fokus auf den Umgang mit Heterogenität oder Inklusion wie folgt beschreiben: „Die Oberflächenstrukturen von Unterricht (Welche Sozialformen und Aktivitäten werden initiiert?), die Tiefenstrukturen von Unterricht (Welche kognitiven Aktivitäten und Wissensfacetten werden wie adressiert und von wem?) und die Strukturierung der Lerngegenstände (In welchen Reihenfolgen, Zugangsweisen und Sinnzusammenhängen sollen welche Inhalte angeboten werden?)“ (Knipping et al., 2017, S. 40, Hervorhebung i.O.). Zur Ausdifferenzierung für einen differenzierenden und inklusiven Mathematikunterricht gehen die Autorinnen davon aus, dass spezifische Lernausgangslagen berücksichtigt werden, „indem allgemeine Qualitätsansprüche und fachdidaktische Kernbestände adaptiert und nicht etwa durch ‚Spezialdidaktiken‘ ersetzt werden“ (Knipping et al., 2017, S. 49). [7]

Aus den obigen Überlegungen zur Betrachtung von Anforderungen durch inklusive Bildung sowohl ausgehend von Aufgaben- und Kompetenzkatalogen als auch ausgehend von der Beschreibung von Kernbeständen für den Umgang mit Heterogenität lassen sich Kompetenzen zur Bewältigung der Anforderungen ableiten. Mit Blick auf das Professionswissen leiten König et al. (2019) Wissen zur Bewältigung von Inklusion ab, das sich aus den Wissensbereichen nach Baumert und Kunter (2011) jeweils erweitert für inklusiven Unterricht zusammensetzt. Wissen und Anforderungen werden dabei nicht als deckungsgleich verstanden, wenn auch Bezüge zwischen einzelnen Anforderungsbereichen und Facetten des professionellen Wissens hergestellt werden können (König et al., 2019). Analog werden aus den zuvor genannten mathematikdidaktischen Kernbeständen weitere Inhalte einzelner Wissensfacetten abgeleitet (Kap. 2.2). Das in diesem Beitrag gewählte Vorgehen in Anlehnung an die Ausführungen von König et al. erscheint nicht zuletzt auch deshalb als tragfähig, weil zum Beispiel nach Bach, Burda-Zoyke und Zinn (2018) einschlägige Veröffentlichungen vorliegen, die im Kontext der veränderten Bedarfe aufgrund von Heterogenität und Inklusion die Kompetenzen der Lehrkräfte zu den Aspekten Diagnostik, Förderung und Beratung als besonders bedeutsam ansehen. [8]

Die Rolle der erweiterten Anforderungen im Kontext der Lehrerbildung und der dazugehörigen Professionalisierung wird vielfach betont, sodass Hillenbrand, Melzer und Hagen (2013) schlussfolgern: die „Gestaltung inklusiver Bildung stellt Aufgaben in allen Kompetenzbereichen, daher sind zur Professionalisierung der Fachkräfte für Inklusion diese Kompetenzen umfassend in den Blick zu nehmen“ (S. 42). Die benötigten Kompetenzen schließen neben Wissen auch Überzeugungen gegenüber Vielfalt ein (vgl. HRK & KMK, 2015). Die Berücksichtigung der Überzeugungen zu Inklusion – zusätzlich zum Professionswissen – ist nicht nur durch den Ansatz von Baumert und Kunter zur Beschreibung der professionellen Handlungskompetenz von Lehrkräften begründet, sondern basiert vor allem auf der Erkenntnis, dass in verschiedenen Studien „ein Zusammenhang zwischen dem Erfolg der Implementation von inklusiven Bildungssettings und der Einstellung und der Bereitschaft der daran Beteiligten postuliert“ (Seifried, 2015, S. 41) wird. Des Weiteren sind motivationale Orientierungen von Bedeutung, da unter Kompetenz nicht nur die Fähigkeit verstanden wird, Anforderungen einer Situation bewältigen zu können, sondern insbesondere auch die Bereitschaft dazu (Kunter, 2011). Im Rahmen eines effektiven Umgangs mit persönlichen Ressourcen beschäftigt sich das Modell nach Baumert und Kunter zudem mit Ausführungen zur Selbstregulation (Klusmann, 2011). Mit Blick auf die erweiterten Anforderungen durch Inklusion scheint eine Berücksichtigung der Motivation und der Selbstregulation von Lehrkräften fortwährend relevant zu sein. [9]

Da Überzeugungen, motivationale Orientierungen und selbstregulative Fähigkeiten unter dem Begriff affektive und motivationale Merkmale zusammengefasst werden können, entsteht insgesamt der in Abbildung 1 skizzierte Ansatz zur Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht. Ohne die erweiterten Bereiche handelt es sich um die gleichen Inhalte der professionellen Handlungskompetenz wie im Modell nach Baumert und Kunter (2006). Die durch gestrichelte Linien gekennzeichneten Kompetenzbereiche verdeutlichen, dass Inhalte der bereits bestehenden Kompetenzbereiche erweitert werden und aufgrund von inklusiver Bildung bereits vorhandene Inhalte besondere Bedeutung erfahren. Der Abbildung kann auch entnommen werden, dass im Bereich „Fachwissen“ durch Inklusion keine weiteren Anforderungen hinzukommen (Kap. 2.2.1). [10]

Die professionelle Handlungskompetenz von Lehrkräften setzt sich aus dem Professionswissen sowie affektiven und motivationalen Merkmalen zusammen. Als Kompetenzbereiche des Professionswissens sind die Bereiche Fachwissen, Pädagogisches Wissen, Fachdidaktisches Wissen, Organisationswissen und Beratungswissen abgebildet. Als Kompetenzbereiche der affektiven und motivationalen Merkmale sind die Bereiche Überzeugungen, Selbstregulation und Motivation abgebildet. Außer dem Fachwissen wurde jedem Kompetenzbereich eine inklusive Erweiterung hinzugefügt, zum Beispiel Fachdidaktisches Wissen inklusiv oder Überzeugungen inklusiv (jeweils gekennzeichnet durch gestrichelte Linien). Damit setzt sich die professionelle Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht aus Professionswissen inklusiv sowie affektiven und motivationalen Merkmalen inklusiv zusammen.
Abbildung 1: Ansatz zur Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-)Unterricht

In den folgenden Kapiteln (2.2 & 2.3) geht es darum, die einzelnen Kompetenzbereiche detaillierter zu erläutern und Bezüge zu den geschilderten Anforderungen durch inklusive Bildung herzustellen. Für die Darstellung der professionellen Handlungskompetenz von Lehrkräften im Regelunterricht orientieren wir uns an der COACTIV-Studie (z.B. Baumert & Kunter, 2006; Krauss et al., 2011). Dabei konzentrieren wir uns auf zentrale Merkmale der einzelnen Kompetenzbereiche, die vor allem im Rahmen der Weiterentwicklung für inklusiven (Mathematik-)Unterricht an Bedeutung gewinnen. Ausgehend von den geschilderten Anforderungen durch inklusive Bildung wird im Anschluss jeweils die inklusive Erweiterung fokussiert. Da einerseits bezogen auf die Bereiche Organisations- und Beratungswissen sowie Selbstregulation und Motivation vergleichsweise wenig Erkenntnisse im Kontext inklusiven Mathematikunterrichts vorliegen und andererseits das fachdidaktische Wissen in diesem Beitrag eine besondere Rolle einnimmt, werden die einzelnen Kompetenzbereiche unterschiedlich detailliert dargestellt. [11]

Kompetenzbereiche für inklusiven (Mathematik-)Unterricht – Professionswissen

Das Professionswissen und die einzelnen Wissensbereiche werden im Folgenden anhand der vielfach verwendeten Unterscheidung von Fachwissen, pädagogischem Wissen, fachdidaktischem Wissen, Organisationswissen und Beratungswissen nach Baumert und Kunter (2006) genauer betrachtet. [12]

Fachwissen

Das Fachwissen wird im Rahmen von COACTIV theoretisch anhand von vier Formen mathematischen Wissens ausdifferenziert: „akademisches Forschungswissen, ein profundes mathematisches Verständnis der in der Schule unterrichteten Sachverhalte, Beherrschung des Schulstoffes auf einem zum Ende der Schulzeit erreichten Niveau und mathematisches Alltagswissen von Erwachsenen, das auch nach Verlassen der Schule noch präsent ist“ (Baumert & Kunter, 2006, S. 495). Das Fachwissen stellt eine zentrale Grundlage für fachdidaktisches Handeln und einen gelingenden (Mathematik-)Unterricht dar (Krauss et al., 2011). Dies gilt sowohl im Regel- als auch im inklusiven (Mathematik-)Unterricht, sodass an dieser Stelle keine Weiterentwicklung im Sinne von „Fachwissen inklusiv“ vorgenommen wird. [13]

Pädagogisches Wissen (inklusiv)

In dem Review von Voss, Kunina-Habenicht, Hoehne und Kunter (2015) wird pädagogisches Wissen definiert als „Kenntnisse über das Lernen und Lehren, die sich auf die Gestaltung von Unterrichtssituationen beziehen und die fachunabhängig, das heißt auf verschiedene Fächer und Bildungsbereiche anzuwenden sind“ (Voss et al., 2015, S. 187). Die Autorinnen beziehen sich unter anderem auf die COACTIV-Studien und identifizieren verschiedene inhaltliche Facetten des pädagogischen Wissens (Voss et al., 2015, S. 194), die für die weiteren Ausführungen zugrunde gelegt werden: [14]

  • Lernen und Lernende

    • Lernprozesse (lern-, motivations- und emotionspsychologisches Wissen)

    • Unterschiede in den Voraussetzungen der Lernenden (Heterogenität)

    • Altersstufen und Lernbiographien (entwicklungspsychologisches Wissen)

  • Umgang mit der Klasse als komplexem sozialen Gefüge

    • Klassenführung

    • Interaktion und soziale Konflikte

  • methodisches Repertoire [15]

    • Lehr-Lern-Methoden und deren lernzieladäquate Orchestrierung

    • Individual- und Lernprozessdiagnostik

    • räumliche, materiale und mediale Gestaltung von Lernumgebungen. [16]

Die grundlegende Idee des Umgangs mit Heterogenität spiegelt sich an vielen Stellen – z.B. im Wissen über Unterschiede in den Voraussetzungen der Lernenden – in den Facetten zum pädagogischen Wissen wider. Neben den Aspekten zum Umgang mit Heterogenität gewinnen folgende Überlegungen im inklusiven Unterricht an Bedeutung: Die Erweiterung des pädagogischen Wissens für inklusiven Unterricht bezieht sich nach König et al. (2019) insbesondere auf die Anforderungsbereiche Diagnose und Intervention. Einen maßgeblichen Ausgangspunkt dafür bilden die oben genannten, von Voss et al. identifizierten, Inhalte der Facetten des pädagogischen Wissens (König et al., 2019). König et al. systematisieren dabei diese Inhalte neu und unterteilen das pädagogische Wissen zum Anforderungsbereich Diagnose in Wissen über Dispositionen und Unterschiede, Wissen über Lernprozesse und methodisches Wissen über Diagnose. Das pädagogische Wissen wird für inklusiven Unterricht dabei insbesondere erweitert um Wissen für diagnostische Klärungen von sonderpädagogischen Förderbedarfen (König et al., 2019). Demnach sehen wir das pädagogische Wissen über Lernen und Lernende sowie die Individual- und Lernprozessdiagnostik des methodischen Repertoires nach Voss et al. als Aspekte des Anforderungsbereichs Diagnose an. Die übrigen Inhalte des pädagogischen Wissens ordnen wir dem Anforderungsbereich Intervention zu. Für inklusiven Unterricht wird das pädagogische Wissen in Bezug zum Anforderungsbereich Intervention nach König et al. (2019) um Wissen über Klassenführung in herausfordernden Situationen inklusiver Settings ergänzt. Demnach unterscheiden König et al. (2019) bezüglich des Anforderungsbereichs Intervention für pädagogisches Wissen im inklusiven Unterricht die folgenden Bereiche: Wissen über Klassenführung, Wissen über Strukturierung und Wissen über Binnendifferenzierung/Individualisierung. An dieser Stelle heben wir Wissen über Differenzierungsmaßnahmen hervor. [17]

Knipping et al. (2017) benennen pädagogische Kernbestände, die Überschneidungen mit den Ausführungen von König et al. (2019) und Voss et al. (2015) aufweisen, und die wir dem Anforderungsbereich Intervention zuordnen. Im Rahmen der Oberflächenstruktur von (Mathematik-)Unterricht werden beispielsweise die Konstrukte Sozialformen, Methodenvielfalt und Classroom Management bedeutsam (Knipping et al., 2017), die sich im pädagogischen Wissen in den Bereichen Umgang mit der Klasse als komplexem sozialen Gefüge und im methodischen Repertoire wiederfinden lassen. Dafür verweisen Knipping et al. (2017) auf die Prinzipien Balance von individuellem und gemeinsamem Lernen, Handlungsorientierung und affektive Lernendenunterstützung. Während diese Prinzipien im Rahmen des pädagogischen Wissens oftmals als methodische Prinzipien verstanden werden, gilt es diese aus fachdidaktischer Perspektive zu vertiefen (Kap. 2.2.3). [18]

Fachdidaktisches Wissen (inklusiv)

Das fachdidaktische Wissen bezieht sich auf unterrichts- und schülerbezogenes Wissen (Baumert & Kunter, 2006), welches nach COACTIV auf die Aufgabe der Lehrkraft abzielt, mathematische Inhalte für Schülerinnen und Schüler zugänglich zu machen (Krauss et al., 2011). Es werden drei Facetten des fachdidaktischen Wissens unterschieden (Baumert & Kunter, 2006; Krauss et al., 2011): [19]

  • Wissen über das Potenzial von Aufgaben

  • Wissen über multiple Repräsentations- und Erklärungsmöglichkeiten

  • Wissen über Schülervorstellungen. [20]

Mit Blick auf das Wissen über das Potenzial von Aufgaben fokussieren wir für den Umgang mit Heterogenität das in der Literatur vielfach diskutierte Differenzierungspotenzial von Aufgaben – insbesondere solches Wissen, das sich auf offene Differenzierungsformate bezieht. Darunter werden selbstdifferenzierende (offene) Aufgaben verstanden, die Bearbeitungen auf unterschiedlichen Niveaus und mit unterschiedlichen Zugangsweisen ermöglichen (Leuders & Prediger, 2016). Ebenso sehen wir das Wissen über geschlossene Differenzierungsformate als Teil dieser Wissensfacette an. Dabei versucht die Lehrkraft, für jede Schülerin und jeden Schüler ein Lernangebot zu erstellen, das auf ihre beziehungsweise seine Bedürfnisse zugeschnitten ist (Leuders & Prediger, 2016). In Bezug auf die fachdidaktischen Wissensfacetten „multiple Repräsentations- und Erklärungsmöglichkeiten“ und „Schülervorstellungen“ erlangen folgende Ausführungen zu den Kernbeständen für den Umgang mit Heterogenität besondere Bedeutsamkeit: Im Rahmen der Tiefenstruktur von Mathematikunterricht kommt beispielsweise das Prinzip der kognitiven Aktivierung zum Tragen. Unter kognitiver Aktivierung wird das Ausmaß verstanden, in dem Lernende zur geistig aktiven Auseinandersetzung mit dem Lerngegenstand angeregt werden (Knipping et al., 2017). Für die fachspezifische Umsetzung der kognitiven Aktivierung erfolgt insbesondere eine Orientierung am entdeckenden Lernen und am produktiven Üben (Knipping et al., 2017). Bezogen auf die Strukturierung von Lerngegenständen spielt unter anderem das Vielfalts-Prinzip für Zugangsweisen eine wichtige Rolle (Knipping et al., 2017). Nach Leuders und Prediger (2016) werden unter Zugangsweisen unterschiedliche Strategien, Darstellungsformen, Denkstile und Bearbeitungswege zusammengefasst. [21]

Das fachdidaktische Wissen für inklusiven (Mathematik-)Unterricht ist Teil des Wissens zur Bewältigung der Anforderungen Diagnose und Intervention (vgl. König et al., 2019). König et al. (2019) beschreiben in diesem Zusammenhang beispielsweise die Anforderung, dass Lehrkräfte auf individuelle Bedürfnisse durch eine Elementarisierung der Unterrichtsinhalte eingehen. Bezogen auf eine Elementarisierung der Unterrichtsinhalte ist es wichtig, dass auch für Schülerinnen und Schüler mit erheblichen Lernschwierigkeiten die Lerninhalte nicht kleinschrittig und voneinander losgelöst dargeboten werden, sondern dass mathematische Zusammenhänge und Inhalte im Ganzen thematisiert werden (Scherer, 1995). Im Sinne der Kombination von Diagnose und Intervention geht es aus einer mathematikdidaktischen Perspektive vor allem um eine diagnosegeleitete individuelle Förderung der Schülerinnen und Schüler (Prediger, 2016). Für deren Umsetzung ist wiederum eine Strukturierung der Lerngegenstände aus fachdidaktischer Perspektive notwendig (Knipping et al., 2017; Prediger, 2016). [22]

In Verbindung zu den genannten Facetten des fachdidaktischen Wissens schließen wir folgende Überlegungen an: Da das Wissen über Schülervorstellungen zum Beispiel Wissen über typische Schülerfehler beinhaltet und es um die Analyse der Denkprozesse der Lernenden geht, ordnen wir der Systematisierung von König et al. (2019) folgend das Wissen über Schülervorstellungen der Anforderung Diagnose im inklusiven Mathematikunterricht zu. Mit Blick auf die didaktische Aufbereitung der Inhalte kommt das Wissen über multiple Repräsentations- und Erklärungsmöglichkeiten und über das Potenzial von Aufgaben bezogen auf die Anforderung Intervention zum Tragen. Das Entscheidende bei der Betrachtung von fachdidaktischem Wissen für inklusiven Mathematikunterricht scheint jedoch nicht diese Systematisierung zu sein. Zentral ist die Frage, welche Prinzipien zum Umgang mit Heterogenität im inklusiven Mathematikunterricht besondere Bedeutung erlangen. [23]

Ausgehend von den obigen Ausführungen zum fachdidaktischen Wissen können folgende Spezifizierungen erfolgen: Zum Beispiel ist „das Konstrukt der kognitiven Aktivitäten als zentral herauszustellen, da Lernen nur stattfinden kann, wenn bei allen Lernenden gemäß ihren jeweiligen Lernvoraussetzungen adaptiv passende kognitive Aktivitäten angeregt werden“ (Knipping et al., 2017, S. 52, Hervorhebung i.O.). Schließlich wird in einem inklusiven Mathematikunterricht Wert darauf gelegt, dass fachliche Lernprozesse aller Schülerinnen und Schüler gefördert werden, wobei ein aktiv-entdeckendes Lernen vor allem bei besonderen Unterstützungsbedarfen und Schwierigkeiten beim Mathematiklernen erfolgsversprechend erscheint (Häsel-Weide & Nührenbörger, 2017). [24]

Zum fachdidaktischen Wissen im inklusiven Mathematikunterricht zählt auch Wissen zum Lernen am gemeinsamen Gegenstand, da gemeinsames und individuelles Lernen in Balance erfolgen sollen (Häsel-Weide & Nührenbörger, 2017). Im Kontext dieser Balance geht es sowohl um Phasen des gemeinsamen Lernens als auch um individuelle Lernphasen, wobei auch das individuelle Lernen von „größtmöglicher Gemeinsamkeit“ (Scherer, 2017, S. 195) geprägt sein soll. Im Kern der Überlegungen zum Lernen am gemeinsamen Gegenstand steht der Gedanke, dass alle Schülerinnen und Schüler in Kooperation miteinander an einem gemeinsamen Gegenstand lernen, wobei der gemeinsame Gegenstand als zentraler Prozess zu verstehen ist, der hinter den „beobachtbaren Erscheinungen steht und sie hervorbringt“ (Feuser, 1989, S. 32). Dabei arbeiten die Schülerinnen und Schüler auf ihrem jeweiligen Entwicklungsniveau entsprechend ihrer momentanen Denk- und Handlungskompetenzen (Feuser, 1989). Das gemeinsame Mathematiklernen ist dabei notwendigerweise mit einem Austausch unter den Lernenden verbunden, da erst der Austausch den Lernenden das Durchdenken von eigenen und anderen Lernwegen ermöglicht (Korff, 2016). Somit erfährt der Austausch unter den Lernenden im inklusiven Mathematikunterricht eine besondere Bedeutung. [25]

Des Weiteren sind beispielsweise folgende Ideen und Ansätze im inklusiven Mathematikunterricht aus fachdidaktischer Perspektive besonders relevant: Handlungsorientierung, Wechsel der Darstellungen und Ansprechen mehrerer Sinneskanäle (Häsel-Weide & Nührenbörger, 2017). Dabei spielt die bereits angeführte Berücksichtigung verschiedener Zugangsweisen und selbstdifferenzierender Aufgaben eine grundlegende Rolle. Im Sinne eines guten gemeinsamen Mathematikunterrichts gewinnen einzelne Aspekte des fachdidaktischen Wissens vor dem Hintergrund des Umgangs mit Heterogenität und weiter durch inklusive Bildung besondere Bedeutung. [26]

Organisationswissen und Beratungswissen (inklusiv)

Unter Organisationswissen wird Wissen verstanden, das sich auf die Funktionslogik und -fähigkeit des Bildungssystems bezieht (Baumert & Kunter, 2011). Das Organisationswissen für inklusiven Unterricht fließt in die Bewältigung der Anforderung Management und Organisation im inklusiven Kontext ein und geht über den eigentlichen Unterricht hinaus (König et al., 2019). Dabei werden die Facetten Kooperation/Koordination, Schulorganisation/Rechtsstellung und Bildungssysteme/Rechtsstellung unterschieden, wobei eine Kooperation sowohl auf Klassenebene (z.B. zwischen Regelschullehrkraft und Lehrkraft für sonderpädagogische Förderung) als auch auf Schulebene (z.B. Zusammenarbeit in einem multiprofessionellen Team mit außerschulischen Partnern) erfolgen kann. Eine interdisziplinäre Kooperation kann dabei zu einer Vernetzung der Qualitätsansprüche von Inklusionspädagogik und Fachdidaktik genutzt werden (Knipping et al., 2017). An dieser Stelle berücksichtigen wir außerdem, dass die Herausforderung der Inklusion oftmals mit Schulentwicklungsprozessen und einer Arbeit an äußeren Rahmenbedingungen einhergeht. [27]

Auf Beratungswissen sind Lehrkräfte in der Kommunikation mit Laien angewiesen (Baumert & Kunter, 2006). Typische Beratungsanlässe sind Schullaufbahnberatungen, Lernschwierigkeiten oder Verhaltensprobleme (Baumert & Kunter, 2011). Das Beratungswissen für inklusiven Unterricht ist für die Bewältigung der Anforderung Beratung und Kommunikation erforderlich. Im inklusiven Kontext kommt insbesondere die Beratung von Schülerinnen und Schülern sowie deren Eltern im Zusammenhang mit sonderpädagogischen Förderbedarfen zur Geltung. Durch Kooperationsanlässe zwischen Lehrkräften und außerschulischen Partnern – beispielsweise bei einer Entwicklung von gemeinsamen Beratungsangeboten – sehen wir eine Verbindung zwischen Beratungs- und Organisationswissen, sodass die Anforderungsbereiche Management und Organisation sowie Beratung und Kommunikation miteinander verbunden sind. [28]

Kompetenzbereiche für inklusiven (Mathematik-)Unterricht – Affektive und motivationale Merkmale

Neben dem Professionswissen zählen affektive und motivationale Merkmale zur professionellen Handlungskompetenz. Hierbei werden nach Baumert und Kunter (2006) die Merkmale Überzeugungen, Selbstregulation und Motivation näher betrachtet und für inklusiven (Mathematik-)Unterricht spezifiziert. [29]

Überzeugungen (inklusiv)

Für Mathematik werden epistemologische Überzeugungen zur Wissenskonstruktion, Überzeugungen über das Lernen und Lehren in einem schulischen Gegenstandsbereich und selbstbezogene Fähigkeitskognitionen unterschieden (Baumert & Kunter, 2006). Überzeugungen können dabei definiert werden als „überdauernde existentielle Annahmen über Phänomene oder Objekte der Welt, die subjektiv für wahr gehalten werden […] und die Art der Begegnung mit der Welt beeinflussen“ (Voss, Kleickmann, Kunter, & Hachfeld, 2011, S. 235, Hervorhebung i.O.). Zur Erfassung von Lehrerüberzeugungen werden in COACTIV die Aspekte Natur des mathematischen Wissens und Lernen und Lehren von Mathematik unterschieden, sowie jeweils deren lerntheoretische Fundierung (Voss et al., 2011). [30]

Viele Forschungsarbeiten beschäftigen sich mit Überzeugungen zu Inklusion, doch liegt bisher keine einheitliche Konzeptualisierung von Inklusion in diesem Zusammenhang vor (vgl. Grosche, 2015). Im Rahmen von Überzeugungen zu inklusiver Bildung geht Inklusion einher mit der „positive[n] Einstellung, Wertschätzung, Anerkennung und bewusste[n] Bejahung von Heterogenität“ (Grosche, 2015, S. 34). Ausgehend von diesem Verständnis betrachten Strauß und König (2017) berufsbezogene Überzeugungen zur inklusiven Bildung angehender Lehrkräfte. Entlang der Anforderungsbereiche und verschiedenen Definitionen von Inklusion haben Strauß und König (2017) begonnen ein Rahmenmodell berufsbezogener Überzeugungen zu inklusiver Bildung zu erstellen. Die adaptive Förderung von Lernenden mit Förderbedarf im Regelunterricht – in Verbindung mit dem Anforderungsbereich Management und Organisation – wird zum Beispiel durch einen höheren Arbeitsaufwand der Lehrkräfte adressiert (Strauß & König, 2017). [31]

Selbstregulation und Motivation (inklusiv)

Mit Bezug zur psychologischen Funktionsfähigkeit beschreiben Baumert und Kunter (2006) Selbstregulation und Motivation als Bestandteile der professionellen Handlungskompetenz. Beide Bestandteile „sind für die psychische Dynamik des Handelns, die Aufrechterhaltung der Intention und die Überwachung und Regulation des beruflichen Handelns über einen langen Zeitraum verantwortlich“ (Baumert & Kunter, 2006, S. 501). In diesem Zusammenhang wurde zum Beispiel die Selbstregulation mit Blick auf das Belastungserleben betrachtet (Baumert & Kunter, 2006). In COACTIV wurde insbesondere die adaptive Selbstregulation, also „ein erfolgreiches Haushalten mit den eigenen Ressourcen“ (Klusmann, 2011, S. 277), untersucht. Unter motivationalen Merkmalen werden vor allem unterschiedliche Ziele, Präferenzen und Motive einzelner Lehrkräfte verstanden (Kunter, 2011). Befunde gibt es insbesondere zu Selbstwirksamkeitserwartungen. Beispielsweise können hohe Selbstwirksamkeitserwartungen ein förderlicher Faktor für die Bewältigung von Anforderungen sein (Kunter, 2011). [32]

Es ist bereits angeklungen, dass die Bereitschaft, inklusive Bildung umsetzen zu wollen, eine entscheidende Rolle für die erfolgreiche Umsetzung von Inklusion spielt. Insbesondere liegen Untersuchungen mit Bezug zu Selbstwirksamkeitserwartungen im inklusiven Unterricht vor: Zum Beispiel weisen Lehrkräfte, die sich als selbstwirksamer einschätzen, positivere Einstellungen zu Inklusion auf (Seifried, 2015). Mit Blick auf die Selbstregulation für inklusiven Unterricht kommt angesichts der wachsenden Anforderungen auch dem Belastungserleben bzw. dem schonenden Umgang mit eigenen Ressourcen eine neue Rolle zu. Sorgen werden von Lehrkräften zum Beispiel dahingehend geäußert, dass sie Angst haben, nicht allen Schülerinnen und Schülern gerecht werden zu können, oder zu wenig Zeit haben, um die individuellen Bedürfnisse der Lernenden berücksichtigen bzw. eine entsprechende Vorbereitung leisten zu können (Seifried, 2015). Bezüglich der Motivation inklusiv kann festgehalten werden, dass die intrinsische Motivation, sich mit inklusionspädagogischen Fragestellungen zu beschäftigen, einen Einfluss auf gelingenden inklusiven Unterricht haben kann (Hellmich & Görel, 2014). [33]

Identifizierte Kompetenzbereiche bei Lehrkräften zu Beginn einer Fortbildung

In diesem Kapitel wird der Frage nachgegangen, inwiefern sich das erweiterte Modell als tragfähig erweist, um Kompetenzbereiche bei Lehrkräften zu Beginn einer Fortbildung zu identifizieren, indem das erweiterte Modell als theoriegeleitetes systematisches Analyseinstrument genutzt wird. Wir verstehen diese Fragestellung dabei als eine Möglichkeit, das anhand der bisherigen theoriebasierten Überlegungen erweiterte Modell für eine Datenanalyse beispielhaft in der Empirie anzuwenden. [34]

Teilnehmende und Fragebogen

Der Auswertung für diesen Beitrag liegen die Daten von 25 Lehrkräften zugrunde, die im inklusiven Mathematikunterricht der Sekundarstufe I tätig sind. Sie nahmen an einer zweijährigen Fortbildung zu inklusivem Mathematikunterricht teil und bearbeiteten den Fragebogen – dessen Fragen die Grundlage für diesen Beitrag bilden – vor Fortbildungsbeginn. Die offenen Fragen des Fragebogens geben den Lehrkräften die Möglichkeit, zu beschreiben, wie sie ihren inklusiven Mathematikunterricht bisher gestalten, mit welcher Motivation sie in die Fortbildung gehen, und welches Ziel sie im Rahmen der Fortbildung verfolgen. Im Einzelnen sind dies folgende Fragen: [35]

  • Mit welchen didaktischen und methodischen Elementen gestalten Sie Ihren inklusiven Mathematikunterricht bisher?

  • Wie beabsichtigen Sie Ihren inklusiven Mathematikunterricht didaktisch und methodisch weiterzuentwickeln?

  • Warum nehmen Sie an dieser Fortbildung teil?

  • Dieses persönliche Lernziel möchte ich im Rahmen der Fortbildung verfolgen. [36]

Unter Zuhilfenahme der zuvor beschriebenen theoriebasierten Überlegungen ist der Fragebogen derart konzipiert worden, dass verschiedene Kompetenzbereiche in den Antworten der Lehrkräfte identifiziert werden können. Demnach können auf die erste Frage zur didaktisch-methodischen Gestaltung insbesondere pädagogische und fachdidaktische Wissensfacetten für inklusiven Mathematikunterricht benannt werden. Hingegen legen die letzten beiden Fragen auch Antworten nahe, die sich auf die Kompetenzbereiche Überzeugungen sowie Selbstregulation und Motivation beziehen. Ebenso ist es denkbar, dass fragenübergreifend Kompetenzbereiche identifiziert werden können. [37]

Datenauswertung

Für die Datenauswertung erfolgte eine (inhaltlich strukturierende) qualitative Inhaltsanalyse in Anlehnung an Mayring (2010). Die Methodik der qualitativen Inhaltsanalyse wird als „kategoriengeleitete Textanalyse“ (Mayring, 2010, S. 13, Hervorhebung i.O.) verstanden. Das Ausgangsmaterial bildeten die digitalisierten Antworten der Lehrkräfte auf die offenen Fragen. Eine Kodiereinheit stellt bereits ein einzelnes Wort dar, da die Lehrkräfte teilweise in Stichworten geantwortet haben. Die Kontexteinheit besteht aus einer gesamten Antwort einer Lehrkraft auf eine der Fragen (Kap. 3.1). Die Antworten der Lehrkräfte wurden für jede Frage nacheinander kodiert und bestehen durchschnittlich aus 2-3 Sätzen/Stichworten pro Frage (wobei die Antworten auf die Frage zur didaktisch-methodischen Gestaltung am ausführlichsten und die Antworten auf die Lernzielformulierung am kürzesten ausfallen). [38]

Ziel der in diesem Beitrag gewählten Vorgehensweise ist die Strukturierung und Einschätzung des Materials anhand vorher festgelegter Ordnungskriterien, sodass bestimmte Inhalte aus dem Material herausgefiltert werden (vgl. strukturierende Inhaltsanalyse nach Mayring, 2010). An dieser Stelle wird der Ablauf unserer Datenauswertung näher betrachtet. Nach einer ersten Materialsichtung erfolgte eine Kodierung des Materials ausgehend von den folgenden aus dem Modell abgeleiteten Kategorien (vgl. Kap. 2.2 & 2.3): [39]

  • für das Professionswissen: Fachwissen, pädagogisches Wissen, fachdidaktisches Wissen sowie Organisationswissen und Beratungswissen

  • für affektive und motivationale Merkmale: Überzeugungen sowie Selbstregulation und Motivation. [40]

In einem weiteren Schritt wurden die zugeordneten Textstellen zu den einzelnen Kategorien mit Blick auf die erweiterten Kompetenzbereiche analysiert. Dafür wurde bei jeder kodierten Textstelle entschieden, ob sie Aspekte der erweiterten Kompetenzbereiche enthält oder nicht. Konkret bedeutet dies, dass untersucht wurde, welche Inhalte der Kategorien unter Inklusionsgesichtspunkten besondere Relevanz bekommen. Anschließend wurden dafür gemeinschaftlich Ankerbeispiele mit dem Fokus auf Wissensbereiche bzw. affektiv-motivationale Merkmale zum Umgang mit Heterogenität und insbesondere zur Bewältigung inklusiver Anforderungen ausgewählt, die es im folgenden Kapitel ebenfalls näher zu erläutern gilt. [41]

Ergebnisse

In den Äußerungen der Lehrkräfte konnten keine Aspekte des Fachwissens identifiziert werden. Eine Übersicht der Ankerbeispiele zu den identifizierten Kompetenzbereichen aus dem erweiterten Modell kann Tabelle 1 entnommen werden. [42]

Tabelle 1: Übersicht über Ankerbeispiele zu identifizierten erweiterten Kompetenzbereichen bei Lehr­kräften zu Beginn einer Fortbildung
Professionelle Handlungskompetenz (inklusiv) Ankerbeispiele
Professionswissen (inklusiv) Fachwissen(inklusiv) -
Pädagogisches Wissen (inklusiv) (1) Unterschiedliche Zeitvorgaben zum Erreichen eines Lernziels zulassen
(2) Starke und schnelle Schülerinnen und Schüler dürfen Langsameren helfen
Fachdidaktisches Wissen (inklusiv) (3) Offene Aufgaben mit verschiedenen Lösungsmöglichkeiten
(4) Einstiege differenziert aufsetzen, sodass Schülergruppen auf unterschiedlichsten Niveaus dennoch alle etwas entdecken und zum Lernprozess beitragen können
(5) Schülerinnen und Schülern mit Förderbedarf Lernen gute Grundlagen vermitteln (Grundrechenarten, Geometrie)
Organisationswissen und Beratungswissen (inklusiv) (6) Teamteaching
(7) Gemeinsam mit meinem Schulteam Ziele formulieren, um sie mit ins Kollegium zu tragen, damit ein Förder- und Forderkonzept entwickelt werden kann
(8) Vorbereitung auf autarkes Erwachsenenleben
Affektive & motivationale Merkmale (inklusiv) Überzeugungen (inklusiv) (9) Allen Schülerinnen und Schülern gerecht werden
(10) Immer wenn es geht, wird kein Unterschied gemacht und es bekommen alle diejenigen Schülerinnen und Schüler zusätzliche Hilfestellung, die es benötigen
Selbstregulation und Motivation (inklusiv) (11) Ich wünsche mir Ideen zur Entlastung im Unterrichtsprozess
(12) Vereinfachung/Effektivität der Vorbereitungszeit

Im Rahmen des pädagogischen Wissens (inklusiv) erlangen Differenzierungsformate für den Umgang mit Heterogenität, die sich beispielsweise auf die Lernzeit beziehen, eine besondere Bedeutung (Bsp. (1)). Ebenso zählen Äußerungen, dass sich Schülerinnen und Schüler gegenseitig helfen, zu dieser erweiterten Kategorie (Bsp. (2)). Dies sind Äußerungen, die wir im Zusammenhang mit dem Wissen über das methodische Repertoire sehen. Andere Facetten des pädagogischen Wissens für inklusiven Unterricht nach König et al. (2019) wie zum Beispiel methodisches Wissen über Diagnose konnten in den Äußerungen der Lehrkräfte nicht identifiziert werden. Insgesamt lassen sich die identifizierten Kompetenzbereiche überwiegend den Wissensfacetten zuordnen, die für die Bewältigung der Anforderung Intervention genutzt werden. An dieser Stelle sei bereits angemerkt, dass dies darin begründet sein könnte, dass es keine explizite Frage zur Diagnose gab, während die Frage zur didaktisch-methodischen Gestaltung des inklusiven Mathematikunterrichts eine Nennung von Aspekten zum Anforderungsbereich Intervention nahelegt. Darüber hinaus konnten bei den Lehrkräften ebenfalls mit Bezug zum Anforderungsbereich Intervention unter anderem Nennungen zu den Aspekten Sozialform (z.B. „Partner- und Gruppenarbeit“) und Methoden (z.B. „Stationsarbeit“) identifiziert werden. [43]

Mit Blick auf das fachdidaktische Wissen (inklusiv) konnten unter Heterogenitätsgesichtspunkten insbesondere Nennungen zum Einsatz offener Aufgaben im inklusiven Mathematikunterricht identifiziert werden (Bsp. (3)). In einer weiteren Äußerung wird deutlich, dass das Ziel der Differenzierung sich darin niederschlägt, dass alle Lernenden auf verschiedenen Niveaus am Mathematikunterricht teilnehmen können (Bsp. (4)). An dieser Stelle wird deutlich, dass das fachdidaktische Wissen zur Balance aus individuellem (hier „auf unterschiedlichsten Niveaus“) und gemeinsamem Lernen (hier „alle etwas entdecken und […] beitragen können“) eine Spezifizierung des pädagogischen Wissens zu diesem Prinzip darstellt. Die aus theoretischen Überlegungen entstandene Betonung der sozialen Austauschprozesse unter den Lernenden konnten in den bisherigen Äußerungen eher im Sinne der Sozialform Gruppenarbeit (pädagogisches Wissen) anstatt unter dem Fokus von mathematikdidaktischen Überlegungen (fachdidaktisches Wissen) identifiziert werden. Zudem äußern die Lehrkräfte Aspekte, die sich einerseits auf spezifische Förderbedarfe beziehen, und andererseits eine Verbindung zur Sicherung von Verstehensgrundlagen aufweisen (Bsp. (5)). Ebenso spiegelt sich in einzelnen Äußerungen die besondere Relevanz der Prinzipien Darstellungsvernetzung und Handlungsorientierung wider. Zum Beispiel konnten Nennungen mit Bezug zu Darstellungsvernetzung und verschiedenen Zugangsweisen identifiziert werden (z.B. „EIS-Prinzip“, also enaktiv, ikonisch, symbolisch). Außerdem lassen sich in den Äußerungen der Lehrkräfte Bezüge zu Anschauungsmaterial (z.B. „Bruchkreise“) im Sinne einer Handlungsorientierung wiederfinden. Des Weiteren benennen die Lehrkräfte, dass ein Praxisbezug hergestellt wird oder die Schülerinnen und Schüler selbst Strategien zur Problemlösung entwickeln. An dieser Stelle wird deutlich, dass weitere, über unsere bisherigen Überlegungen hinausgehende, fachdidaktische Facetten unter inklusionsspezifischen Gesichtspunkten relevant werden, und dass andere theoretisch bedeutsame Facetten (z.B. das Lernen am gemeinsamen Gegenstand) zu diesem Zeitpunkt kaum auftreten. Ähnlich wie beim pädagogischen Wissen (inklusiv) beziehen sich die hier identifizierten Inhalte auf den Anforderungsbereich Intervention. [44]

Aspekte des Organisationswissens (inklusiv) konnten beispielsweise in Form von Nennungen zum Teamteaching identifiziert werden (Bsp. (6)). In den Antworten lassen sich unter Inklusionsgesichtspunkten vor allem Äußerungen erkennen, die sich auf die Zusammenarbeit zwischen Regel- und Förderschullehrkraft sowie auf die Arbeit an Schulentwicklungsprozessen beziehen (Bsp. (7)). Weitere identifizierte Aspekte beziehen sich auf den Austausch mit Kolleginnen und Kollegen, das Voranbringen des Schulkonzeptes und die Weitergabe neuer Ideen im Kollegium. Dem Beratungswissen (inklusiv) konnte ausgehend von dem Aspekt der Schullaufbahn- und Berufsberatung eine Äußerung einer Lehrkraft zugeordnet werden, in der der Anspruch einer Vorbereitung auf ein autarkes Erwachsenenleben formuliert wird (Bsp. (8)). Weitere Aspekte des Beratungswissens konnten in den Äußerungen der Lehrkräfte nicht identifiziert werden. [45]

Als Überzeugungen (inklusiv) im Zusammenhang mit inklusiver Bildung konnte in den Äußerungen der Lehrkräfte insbesondere der Wunsch identifiziert werden, allen Schülerinnen und Schülern gerecht werden zu wollen, und allen Lernenden gemäß ihren Voraussetzungen Hilfestellungen bieten zu können (Bsp. (9) & (10)). Darüber hinaus äußern die Lehrkräfte zum Beispiel, dass Mathematik Spaß machen sollte, oder wie Kinder lernen sollen (z.B. „Hilf mir es selbst zu tun.“). [46]

Mit Blick auf die Kompetenzbereiche Selbstregulation und Motivation (inklusiv) wurden unter Inklusionsgesichtspunkten einerseits vor allem Aspekte der adaptiven Selbstregulation (Bsp. (11) & (12)) und andererseits Aspekte der Motivation, sich mit inklusionspädagogischen Fragestellungen zu beschäftigen (z.B. „um mich persönlich dem Thema näher zu bringen“), identifiziert. Außerdem wird der Wunsch geäußert, allgemein neue Impulse zu bekommen, oder den eigenen Mathematikunterricht zu verbessern. [47]

Zusammenfassend kann festgehalten werden, dass die Lehrkräfte von Maßnahmen zum Umgang mit Heterogenität berichten, wie etwa in Form von Differenzierungsmaßnahmen. Darüber hinaus benennen die Lehrkräfte zum Beispiel individuelles und gemeinsames Lernen, die Zusammenarbeit von Regel- und Förderschullehrkräften und den Gedanken „allen Schülerinnen und Schülern gerecht werden“ als Aspekte, die für inklusiven (Mathematik-)Unterricht von besonderer Bedeutung sind. [48]

Diskussion und Ausblick

Ausgehend von spezifischen Anforderungen inklusiver Settings wurde in diesem Beitrag eine Möglichkeit vorgestellt, wie das Modell zur professionellen Handlungskompetenz von Lehrkräften von Baumert und Kunter (2006) für inklusiven (Mathematik-)Unterricht weiterentwickelt werden kann. Dabei wurden diejenigen Aspekte herausgearbeitet, die durch inklusive Bildung eine besondere Bedeutung erfahren. [49]

Wie zuvor aufgezeigt, liefert das Modell zum Beispiel die Möglichkeit, Kompetenzbereiche bei Lehrkräften bezüglich ihrer Äußerungen zur didaktisch-methodischen Gestaltung ihres inklusiven Mathematikunterrichts und zur Motivation ihrer Fortbildungsteilnahme zu identifizieren. Daraus können Ideen zur Fortbildungsgestaltung zu inklusivem (Mathematik-)Unterricht abgeleitet werden. Werden beispielsweise überwiegend Äußerungen zum pädagogischen Wissen identifiziert, so könnten Fortbildende stärker Aspekte des fachdidaktischen Wissens im Laufe einer Fortbildung einbringen und eine Verbindung zum vorhandenen pädagogischen Wissen zur didaktisch-methodischen Gestaltung des inklusiven Mathematikunterrichts herstellen. Vor allem wenn essentielle Aspekte zur Bewältigung inklusiver Anforderungen nicht benannt werden, ist dies ein Indiz dafür, diese Inhalte in einer Fortbildung grundlegend zu adressieren, um sie den Teilnehmenden präsent(er) zu machen. Bezogen auf die hier betrachteten Fortbildungsteilnehmenden scheint die Thematisierung weiterer Inhalte zum Lernen am gemeinsamen Gegenstand beispielsweise von besonderer Bedeutung zu sein. Spielt etwa das Belastungserleben als Teil der Aspekte der adaptiven Selbstregulation eine tragende Rolle, kann es sinnvoll sein, den verantwortungsvollen Umgang mit eigenen Ressourcen angesichts erweiterter Anforderungen durch inklusive Bildung in einer Fortbildung zu thematisieren. Zukünftig werden wir das Modell insbesondere zur Beschreibung von Lernprozessen von Lehrkräften im Verlauf einer Fortbildung nutzen, um daraus weitere Ideen zur Fortbildungsgestaltung abzuleiten. Im Allgemeinen ist es außerdem möglich, das erweiterte Modell im Kontext anderer Phasen der Lehrerbildung zu denken und dadurch bisherige Ausführungen zur Professionalisierung von Fachkräften für inklusive Schulen umfassender zu berücksichtigen (z.B. anhand von Hillenbrand et al., 2013 sowie Heinrich et al., 2013). [50]

Im Folgenden werden einige Limitationen der Modellweiterentwicklung und des Anwendungsbeispiels thematisiert. Für die Weiterentwicklung der Wissensbereiche muss zunächst angemerkt werden, dass die Erweiterung der einzelnen Facetten für inklusiven Unterricht nicht gleichbedeutend mit einer Spezialisierung aus sonderpädagogischer Sicht ist. Demnach kann unter sonderpädagogischem Spezialwissen auch Wissen über Interventionskonzepte bei Lernenden mit spezifischen Behinderungen verstanden werden, in Abgrenzung zu sonderpädagogischem Basiswissen, das durchaus für Regelschullehrkräfte im inklusiven Unterricht relevant ist (König et al., 2019). Darüber hinaus fordern König et al. (2019) ausgehend von der Konzeptualisierung des pädagogischen Wissens für inklusiven Unterricht eine Ergänzung von „Forschungsansätze[n] zur Modellierung und Erfassung situationsspezifischer Fähigkeiten im Bereich der unterrichtlichen Anforderungen inklusiver Bildung und Erziehung, die über die Erfassung von vor allem deklarativem Wissen hinausgehen“ (S. 59). Gleiches gilt für die Ausführungen zu weiteren Wissensbereichen in diesem Beitrag und insbesondere für das fachdidaktische Wissen (inklusiv), zum Beispiel vor dem Hintergrund der Gegenüberstellung von kognitiver und situierter Perspektive (vgl. Depaepe, Verschaffel, & Kelchtermanns, 2013). Des Weiteren weisen die Ausführungen zu den fachdidaktischen Wissensfacetten ausgehend vom Umgang mit Heterogenität Verbindungen zueinander auf, deren Erläuterungen in den bisherigen Überlegungen noch nicht ausgeführt werden konnten. Beispielsweise verdeutlicht der folgende Gedanke im Zusammenhang mit selbstdifferenzierenden Aufgaben die Verbindung von der Balance aus individuellem und gemeinsamem Lernen sowie Zugangsweisen: „[…] im Sinne der Balance von Individualisierung und Kooperation [ist] sowohl die individuelle Erarbeitung entsprechend des jeweils eigenen Zugangs als auch die Anregung durch die Zugangsweisen anderer in gemeinsamen Arbeitsphasen von Bedeutung“ (Knipping et al., 2017, S. 52). Außerdem wird darauf hingewiesen, dass sich die Ausführungen zu den Kernbeständen für den Umgang mit Heterogenität bisher in der Hochschullehre als fruchtbar erwiesen haben, diese aber empirisch noch untermauert werden sollen (Knipping et al., 2017). [51]

In diesem Beitrag wurden literaturbasiert Anforderungen inklusiver Settings betrachtet. Diese Vorgehensweise könnte insofern ergänzt werden, als dass auch Arbeiten existieren, die zusätzlich Interviews mit Expertinnen und Experten heranziehen, um Anforderungen im inklusiven Fachunterricht zu identifizieren (für naturwissenschaftlichen Sachunterricht siehe z.B. Mester, 2019). Außerdem geht eine umfassende Betrachtung aller Kompetenzbereiche für inklusiven (Mathematik-)Unterricht im Rahmen zukünftiger Arbeiten damit einher, einige der in diesem Beitrag nur verkürzt dargestellten Bereiche weiter auszuführen (z.B. Beratungswissen oder Überzeugungen). [52]

An dieser Stelle muss außerdem kritisch angemerkt werden, dass es sich bei der hier verwendeten Datengrundlage um Selbstberichte der Lehrkräfte handelt, von denen nicht automatisch auf tatsächlich vorhandene Kompetenzen bei den Lehrkräften geschlossen werden kann. Da dem Anwendungsbeispiel vergleichsweise wenig umfangreiches Datenmaterial zugrunde liegt, erscheint es sinnvoll, die Tragfähigkeit des Modells an Daten aus vergleichbaren und anderen Kontexten weiter zu untersuchen. Denkbar wäre, dass sich durch mehr Datenmaterial zudem die Möglichkeit ergibt, die einzelnen Kompetenzbereiche noch weiter zu spezifizieren. [53]

Literatur

  1. Bach, A., Burda-Zoyke, A. & Zinn, B. (2018). Inklusionsbezogene Handlungsfelder und Kompetenzen von (angehenden) Lehrkräften an beruflichen Schulen. In Bundesministerium für Bildung und Forschung (Hrsg.), Perspektiven für eine gelingende Inklusion. Beiträge der „Qualitätsoffensive Lehrerbildung“ für Forschung und Praxis (S. 120–131). BerlinAbgerufen unter: https://www.bmbf.de/upload_filestore/pub/Perspektiven_fuer_eine_gelingende_Inklusion.pdf.
  2. Baumert, J. & Kunter, M. (2006). Stichwort: Professionelle Kompetenz von Lehrkräften. Zeitschrift für Erziehungswissenschaft, 9(4), 469–520. doi: 10.1007/s11618-006-0165-2.
  3. Baumert, J. & Kunter, M. (2011). Das Kompetenzmodell von COACTIV. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV (S. 29–53). Münster: Waxmann.
  4. Depaepe, F., Verschaffel, L. & Kelchtermanns, G. (2013). Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teaching and Teacher Education, 34, 12–25. doi: 10.1016/j.tate.2013.03.001.
  5. Feuser, G. (1989). Allgemeine integrative Pädagogik und entwicklungslogische Didaktik. Behindertenpädagogik, 28(1), 4–48.
  6. Fischer, C., Kopmann, H., Rott, D., Veber, M. & Zeinz, H. (2014). Adaptive Lehrkompetenz und pädagogische Haltung. Lehrerbildung für eine inklusive Schule. In K. Zierer (Hrsg.), Jahrbuch für Allgemeine Didaktik 2014. Thementeil Allgemeine Didaktik für eine inklusive Schule. Allgemeiner Teil (S. 16–34). Baltmannsweiler: Schneider Verlag Hohengehren.
  7. Grosche, M. (2015). Was ist Inklusion? Ein Diskussions- und Positionsartikel zur Definition von Inklusion aus Sicht der empirischen Bildungsforschung. In P. Kuhl, P. Stanat, B. Lütje-Klose, C. Gresch, H. A. Pant & M. Prenzel (Hrsg.), Inklusion von Schülerinnen und Schülern mit sonderpädagogischem Förderbedarf in Schulleistungserhebungen (S. 17–39). Wiesbaden: Springer Fachmedien. doi: 10.1007/978-3-658-06604-8.
  8. Häsel-Weide, U. & Nührenbörger, M. (2017). Grundzüge des inklusiven Mathematikunterrichts. Mit allen Kindern rechnen. In U. Häsel-Weide & M. Nührenbörger (Hrsg.), Gemeinsam Mathematik lernen - mit allen Kindern rechnen (S. 8–21). Frankfurt a.M.: Grundschulverband e.V..
  9. Heinrich, M., Urban, M. & Werning, R. (2013). Grundlagen, Handlungsstrategien und Forschungsperspektiven für die Ausbildung und Professionalisierung von Fachkräften für inklusive Schulen. In H. Döbert & H. Weishaupt (Hrsg.), Inklusive Bildung professionell gestalten. Situationsanalyse und Handlungsempfehlungen (S. 69–133). Münster: Waxmann.
  10. Hellmich, F. & Görel, G. (2014). Erklärungsfaktoren für Einstellungen von Lehrerinnen und Lehrern zum inklusiven Unterricht in der Grundschule. Zeitschrift für Bildungsforschung, 4(3), 227–240. doi: 10.1007/s35834-014-0102-z.
  11. Hillenbrand, C., Melzer, C. & Hagen, T. (2013). Bildung schulischer Fachkräfte für inklusive Bildungssysteme. In H. Döbert & H. Weishaupt (Hrsg.), Inklusive Bildung professionell gestalten. Situationsanalyse und Handlungsempfehlungen (S. 33–68). Münster: Waxmann.
  12. HRK, & KMK (2015). Lehrerbildung für eine Schule der Vielfalt: Gemeinsame Empfehlung von Hochschulrektorenkonferenz und Kultusministerkonferenz (Beschluss der Kultusministerkonferenz vom 12.03.2015/Beschluss der Hochschulrektorenkonferenz vom 18.03.2015). Abgerufen unter: https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2015/2015_03_12-Schule-der-Vielfalt.pdf.
  13. Klemm, K. & Preuss-Lausitz, U. (2011). Auf dem Weg zur schulischen Inklusion in Nordrhein-Westfalen. Empfehlungen zur Umsetzung der UN-Behindertenrechtskonvention im Bereich der allgemeinen Schulen. Abgerufen unter: http://www.jugendsozialarbeit.de/media/raw/KLEMM_klaus__auf_dem_weg_zur_schulischen_inklusion_in_nrw.pdf.
  14. Klusmann, U. (2011). Allgemeine berufliche Motivation und Selbstregulation. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV (S. 277–294). Münster: Waxmann.
  15. Knipping, C., Korff, N. & Prediger, S. (2017). Mathematikdidaktische Kernbestände im Umgang mit Heterogenität – Versuch einer curricularen Bestimmung. In C. Selter, S. Hußmann, C. Hößle, C. Knipping, K. Lengnink & J. Michaelis (Hrsg.), Diagnose und Förderung heterogener Lerngruppen – Theorien, Konzepte und Beispiele aus der MINT-Lehrerbildung (S. 39–60). Münster: Waxmann.
  16. König, J., Gerhard, K., Kaspar, K. & Melzer, C. (2019). Professionelles Wissen von Lehrkräften zur Inklusion: Überlegungen zur Modellierung und Erfassung mithilfe standardisierter Testinstrumente. Pädagogische Rundschau, 73(1), 43–64. doi: 10.3726/PR012019.0004.
  17. König, J., Gerhard, K., Melzer, C., Rühl, A.-M., Zenner, J. & Kaspar, K. (2017). Erfassung von pädagogischem Wissen für inklusiven Unterricht bei angehenden Lehrkräften: Testkonstruktion und Validierung. Unterrichtswissenschaft, 45(4), 223–242.
  18. Korff, N. (2016). Inklusiver Mathematikunterricht in der Primarstufe. Erfahrungen, Perspektiven und Herausforderungen (2. Auflage). Baltmannsweiler: Schneider Verlag Hohengehren.
  19. Krauss, S., Blum, W., Brunner, M., Neubrand, M., Baumert, J., Kunter, M., Besser, M. & Elsner, J. (2011). Konzeptualisierung und Testkonstruktion zum fachbezogenen Professionswissen von Mathematiklehrkräften. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV (S. 135–161). Münster: Waxmann.
  20. Kunter, M. (2011). Motivation als Teil der professionellen Kompetenz – Forschungsbefunde zum Enthusiasmus von Lehrkräften. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV (S. 259–276). Münster: Waxmann.
  21. Leuders, T. & Prediger, S. (2016). Flexibel differenzieren und fokussiert fördern im Mathematikunterricht. Berlin: Cornelsen Scriptor.
  22. Mayring, P. (2010). Qualitative Inhaltsanalyse. Grundlagen und Techniken (11. Auflage). Weinheim: Beltz.
  23. Melzer, C., Hillenbrand, C., Sprenger, D. & Hannemann, T. (2015). Aufgaben von Lehrkräften in inklusiven Bildungssystemen – Review internationaler Studien. Erziehungswissenschaft, 26(2), 61–80. doi: 10.3224/ezw.v26i2.21070.
  24. Mester, T. (2019). Inklusionsbezogenes sachunterrichtsdidaktisches Wissen – Ein Modellierungsansatz unter Berücksichtigung der Anforderungen im inklusiven naturwissenschaftlichen Sachunterricht aus der Sicht von Lehrkräften. In D. Pech, C. Schomaker & T. Simon (Hrsg.), Inklusion im Sachunterricht. Perspektiven der Forschung (S. 225–235). Bad Heilbrunn: Klinkhardt.
  25. Moser, V. & Kropp, A. (2014). Abschlussbericht: ,Kompetenzen in inklusiven Settings (KIS) - Vorarbeiten zu einem Kompetenzstrukturmodell sonderpädagogischer Lehrkräfte. Berlin: Humboldt-Universität. Abgerufen unter: https://www.reha.hu-berlin.de/de/lehrgebiete/arp/forschung/moser-kropp_kis_abschlussbericht_2014.03.pdf.
  26. Prediger, S. (2016). Inklusion im Mathematikunterricht. Forschung und Entwicklung zur fokussierten Förderung statt rein unterrichtsmethodischer Bewältigung. In J. Menthe, D. Höttecke, T. Zabka, M. Hammann & M. Rothgangel (Hrsg.), Befähigung zu gesellschaftlicher Teilhabe. Beiträge der fachdidaktischen Forschung (S. 361–372). Münster: Waxmann.
  27. Scherer, P. (1995). Entdeckendes Lernen im Mathematikunterricht der Schule für Lernbehinderte. Theoretische Grundlegung und evaluierte unterrichtspraktische Erprobung. Heidelberg: Edition Schindele.
  28. Scherer, P. (2017). Gemeinsames Lernen oder Einzelförderung? – Grenzen und Möglichkeiten eines inklusiven Mathematikunterrichts. In F. Hellmich & E. Blumberg (Hrsg.), Inklusiver Unterricht in der Grundschule (S. 194–212). Stuttgart: Kohlhammer.
  29. Seifried, S. (2015). Einstellungen von Lehrkräften zu Inklusion und deren Bedeutung für den schulischen Implementierungsprozess – Entwicklung, Validierung und strukturgleichungsanalytische Modellierung der Skala EFI-L [Dissertation] Abgerufen unter: https://opus.ph-heidelberg.de/frontdoor/deliver/index/docId/140/file/Dissertation_Seifried_Stefanie.pdf.
  30. Strauß, S. & König, J. (2017). Berufsbezogene Überzeugungen von angehenden Lehrkräften zur inklusiven Bildung. Unterrichtswissenschaft, 45(4), 243–261.
  31. Voss, T., Kleickmann, T., Kunter, M. & Hachfeld, A. (2011). Überzeugungen von Mathematiklehrkräften. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV (S. 235–257). Münster: Waxmann.
  32. Voss, T., Kunina-Habenicht, O., Hoehne, V. & Kunter, M. (2015). Stichwort Pädagogisches Wissen von Lehrkräften: Empirische Zugänge und Befunde. Zeitschrift für Erziehungswissenschaft, 18(2), 187–223. doi: 10.1007/s11618-015-0626-6.
  33. Weiß, S., Muckenthaler, M., Heimlich, U., Küchler, A. & Kiel, E. (2019). Welche spezifischen Bedarfe einer Qualifizierung und Professionalisierung haben Lehrer\*innen in inklusiven Schulen?. QfI - Qualifizierung für Inklusion, 1(1). doi: 10.21248/QfI.6.

Kontakt:

Jennifer Bertram, Ruhr-Universität Bochum, Fakultät für Mathematik - Didaktik der Mathematik, Universitätsstraße 150, 44780 Bochum
E-Mail: jennifer.bertram@rub.de

Zitation:

Bertram, J., Albersmann, N. & Rolka, K. (2020). Ansatz zur Weiterentwicklung des Modells der professionellen Handlungskompetenz von Lehrkräften für inklusiven (Mathematik-) Unterricht – Identifizierte Kompetenzbereiche bei Lehrkräften zu Beginn einer Fortbildung. QfI - Qualifizierung für Inklusion, 2(1), doi:

Eingereicht:

14.09.2019